.png)

Dr. Philippe XU & Pr. Philippe BONNIFAIT
Ph.D. Thesis Defense - Nov. 12, 2024
- Source: Zoox (Youtube)
Localization for AD
Localization for AD
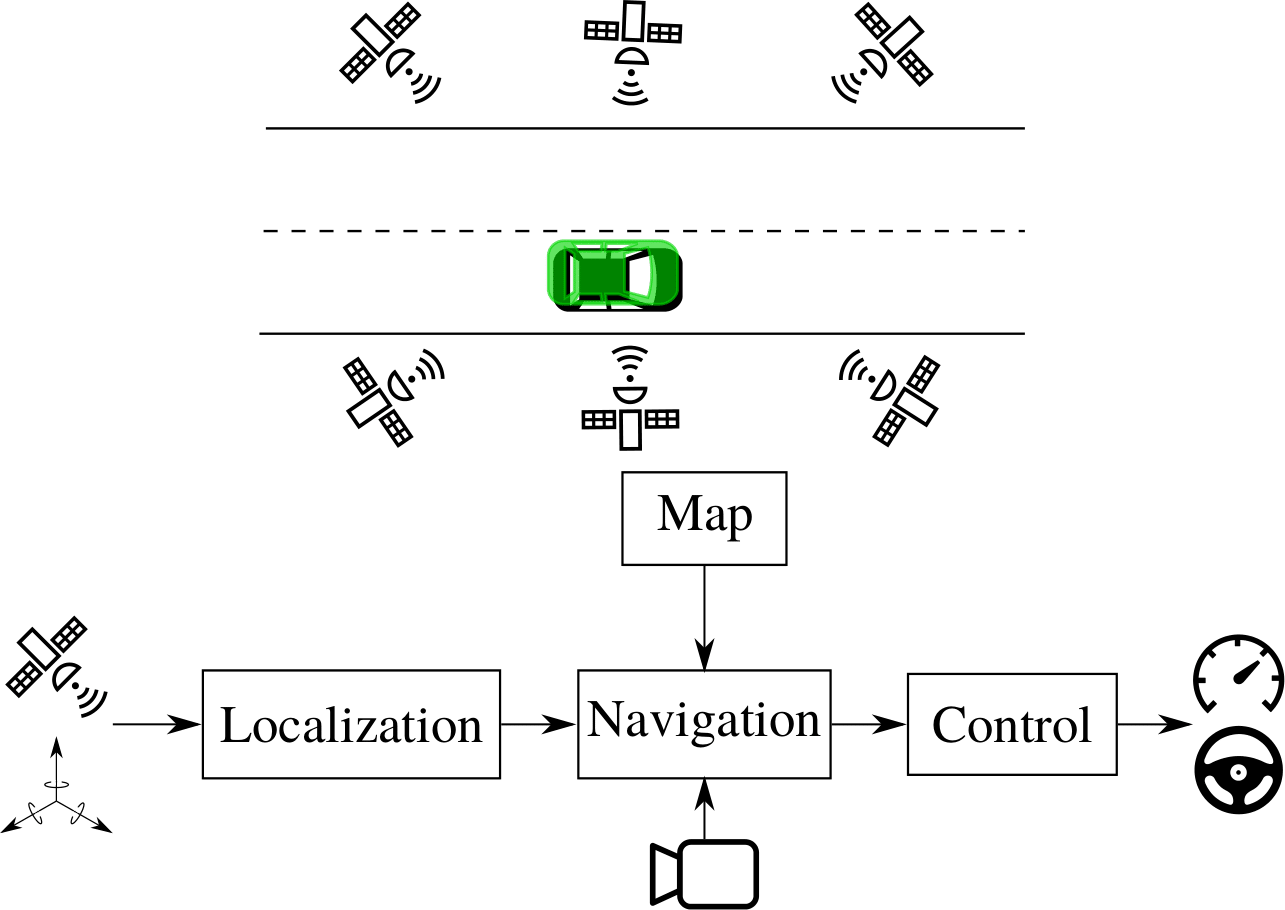
Localization for AD
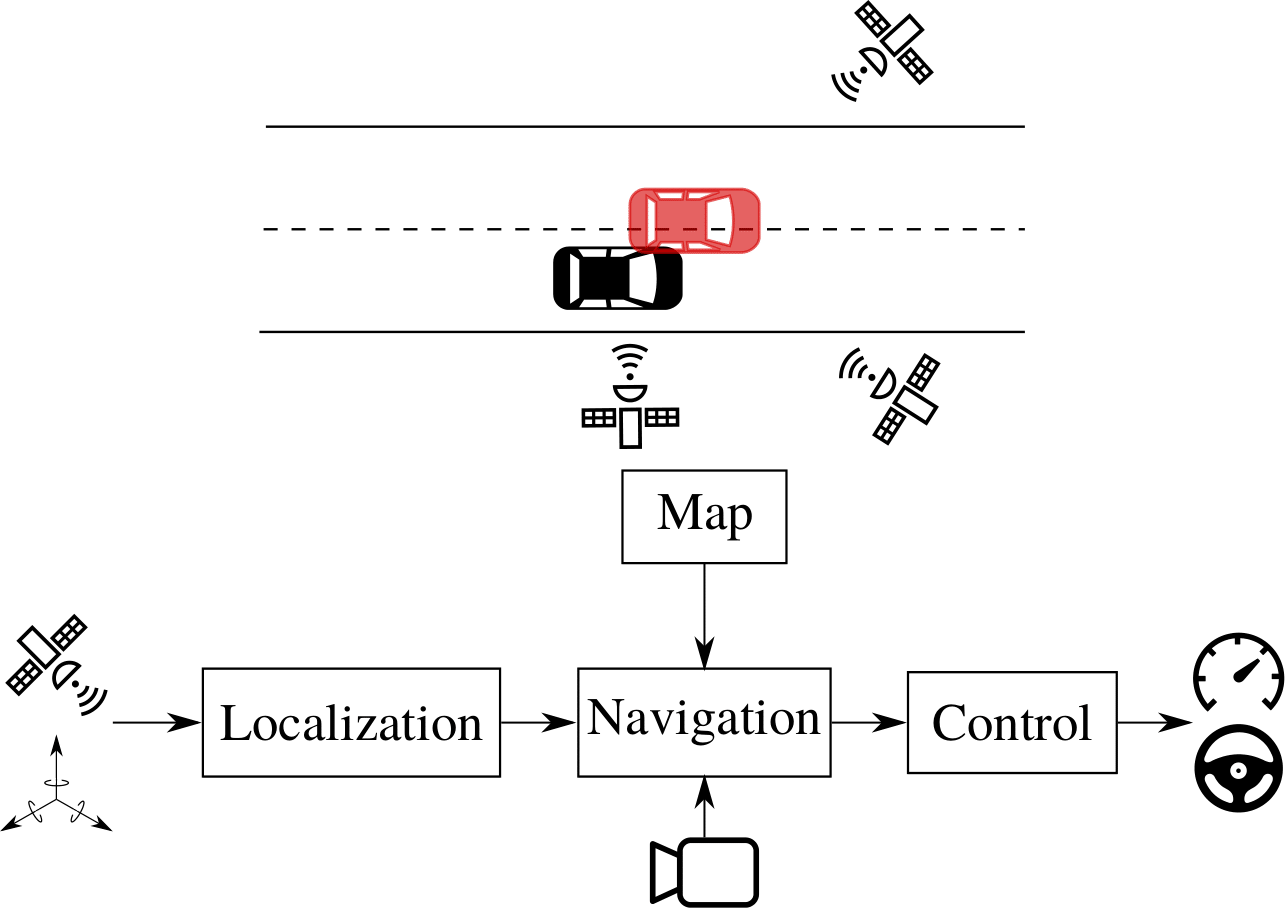
Problem Statement
Problem Statement
Multi-modal Automatic Image Annotation
Training with Pointwise Automatic Annotations
Multi-sensor Localization
Conclusion
HD Maps for localization
- Dense maps
- 👍 High detail
- 👎 High storage, limited scalability, sensor-specific
- Vector maps
- 👍 Lightweight, sensor agnostic
- 👎 low detail

Compiegne HD Map
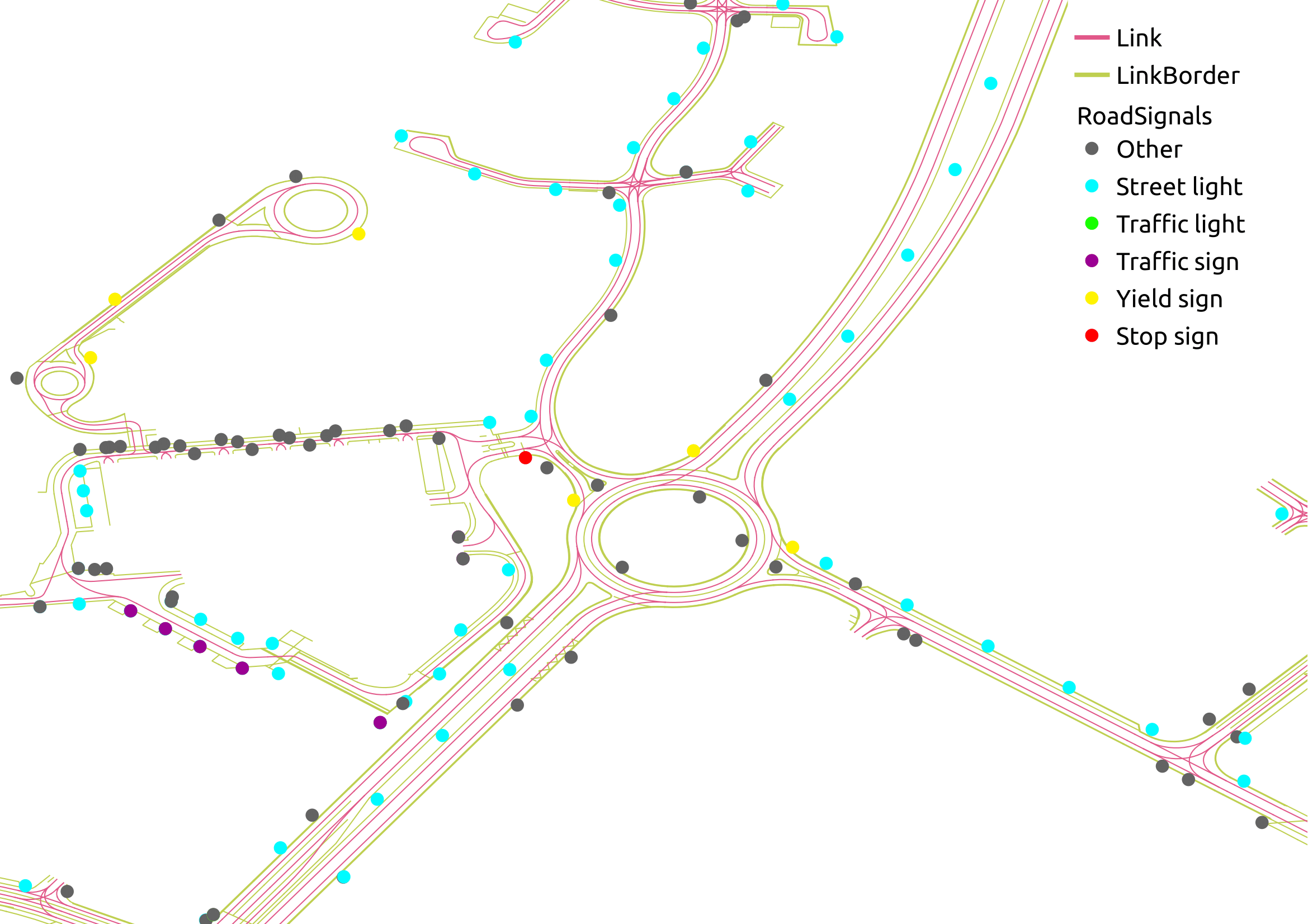
Localization with vector maps
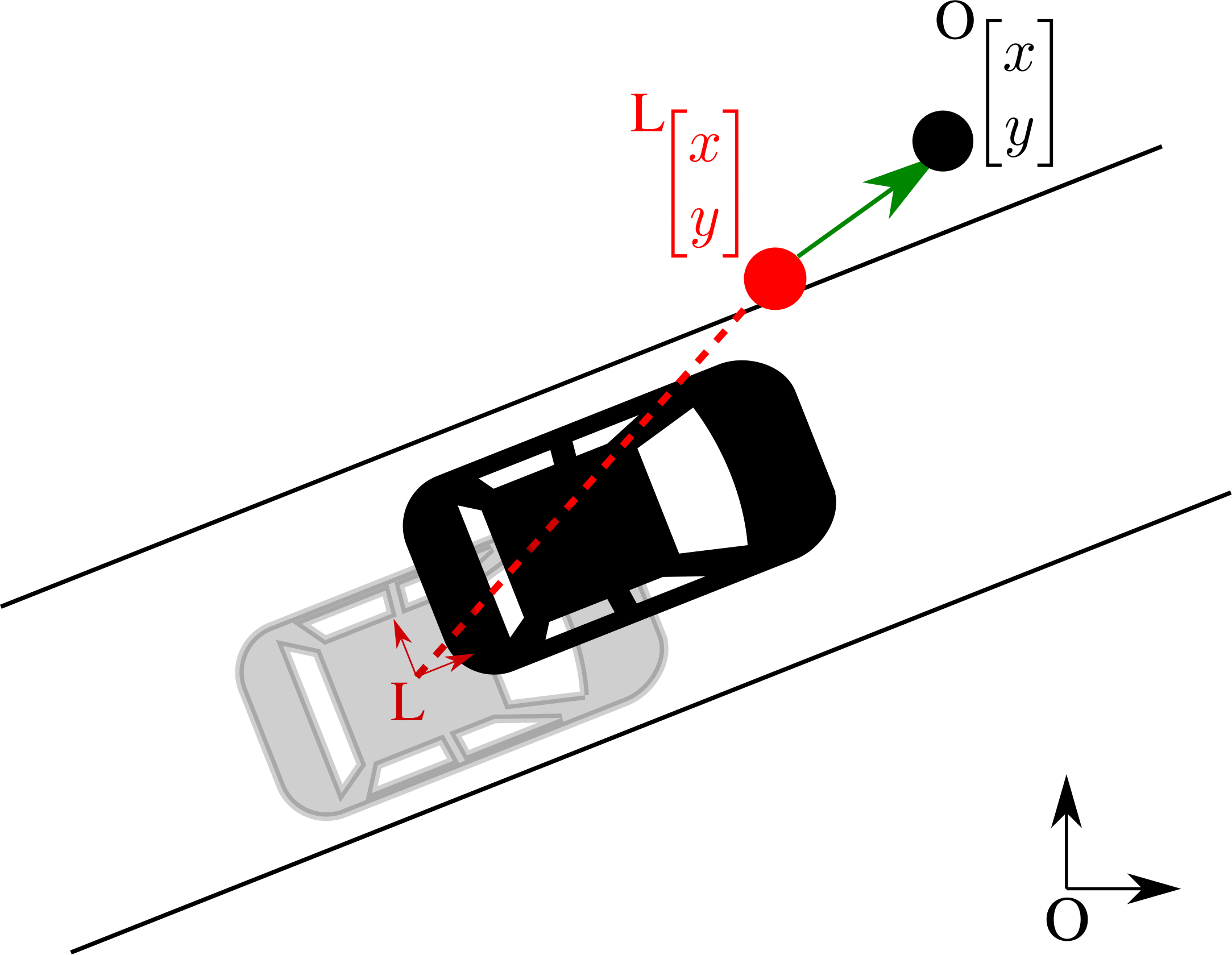
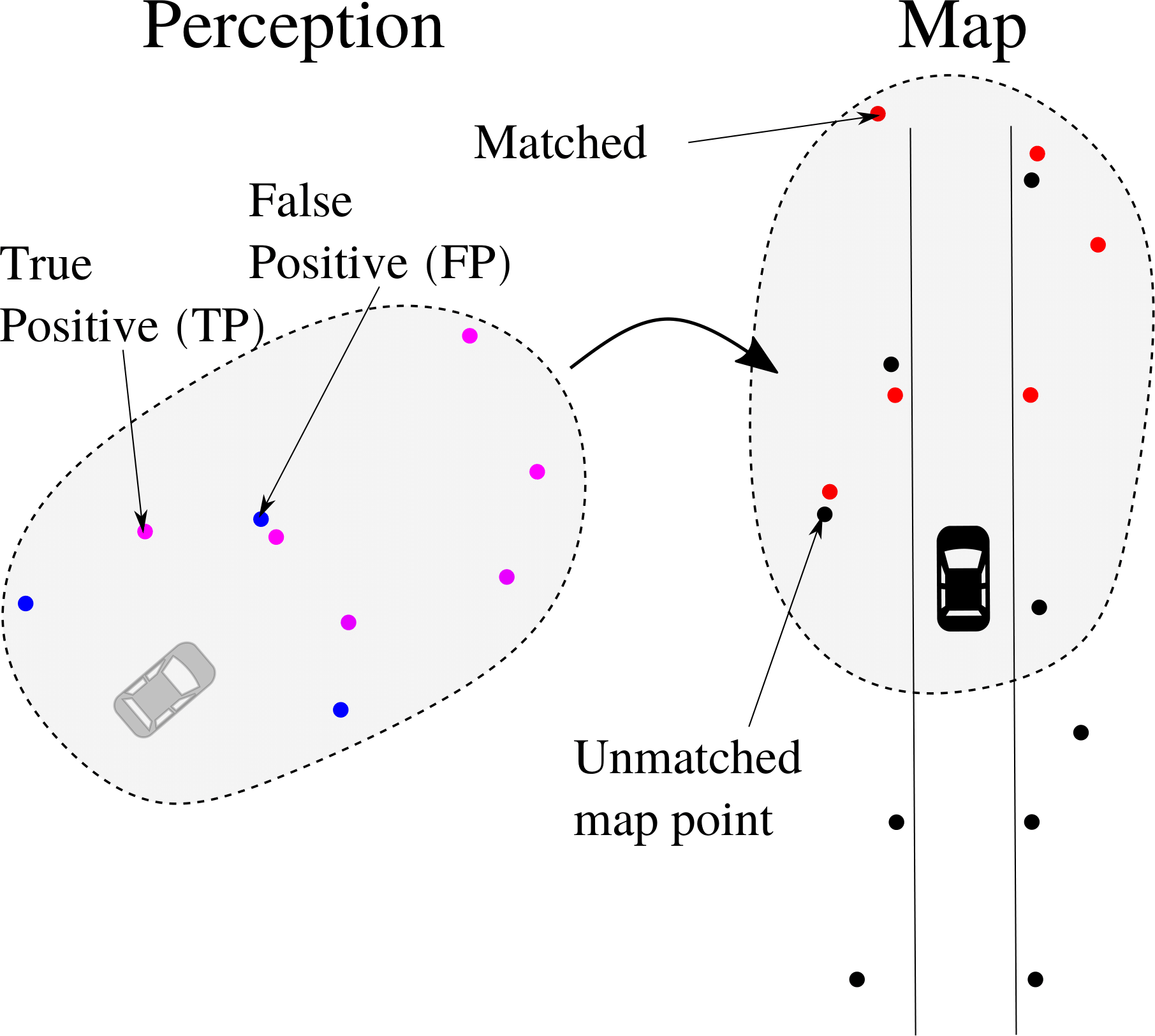
Indiscernible features ⇒ Data association
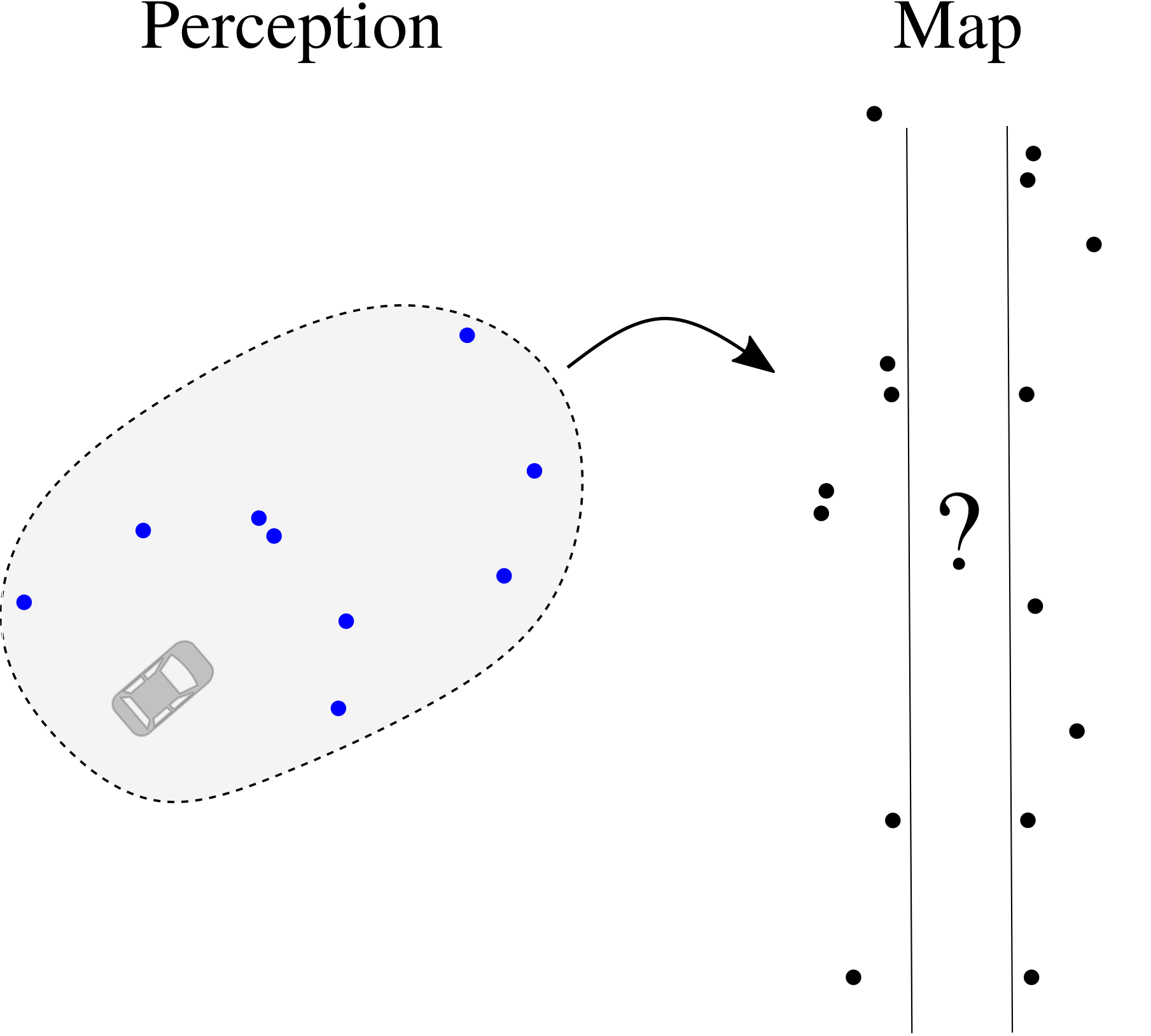
Indiscernible features ⇒ Data association
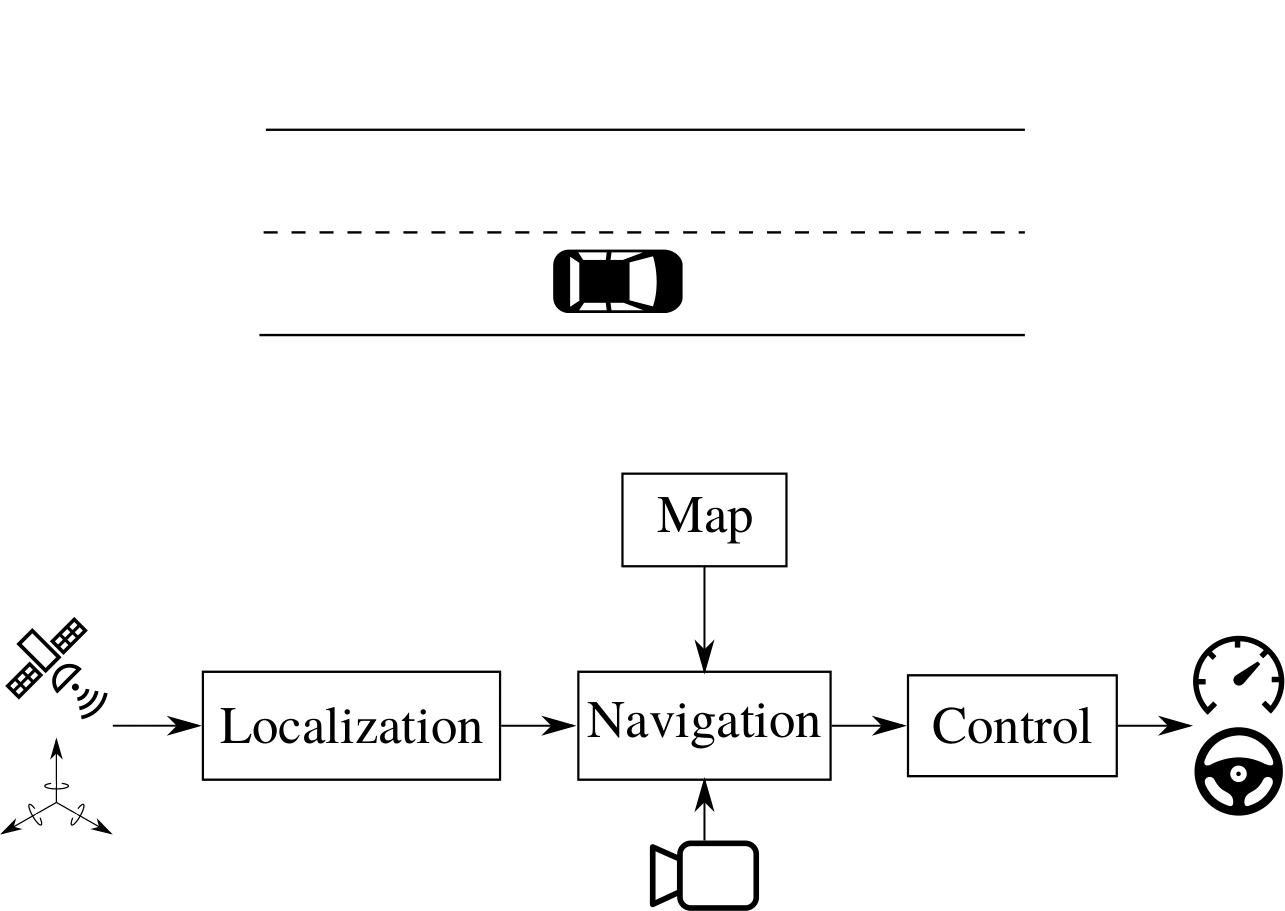
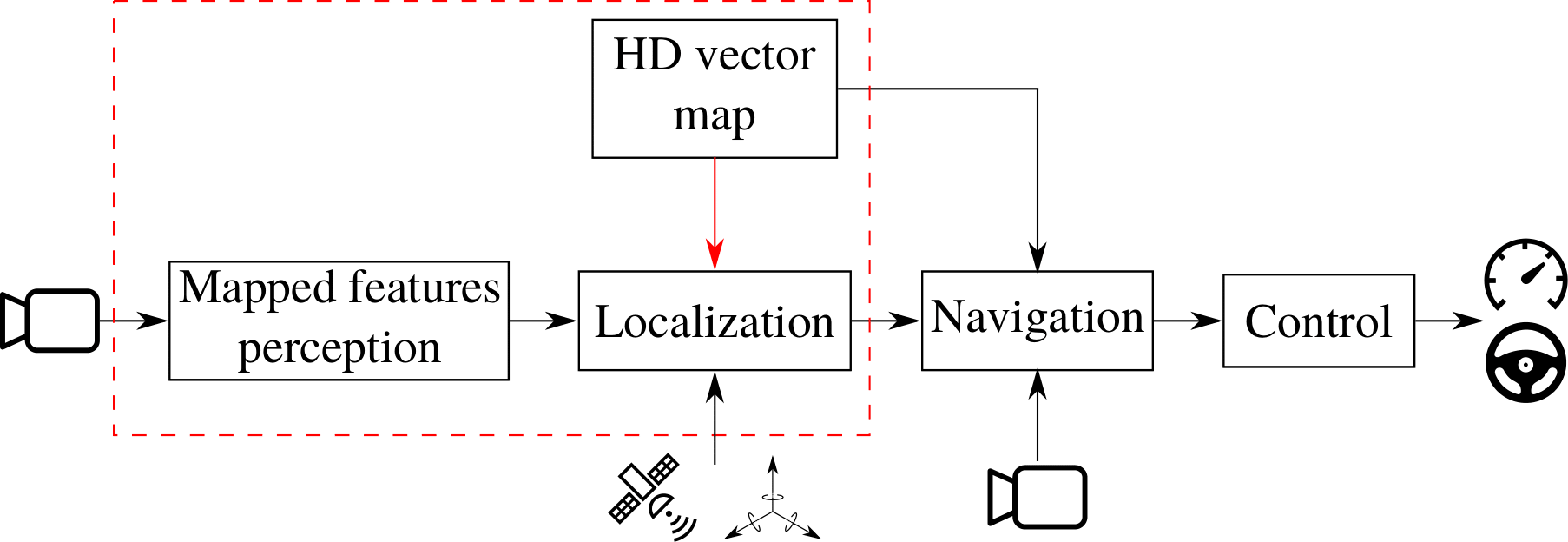
Studied AD pipeline
Mapped features detection

Geometric approaches
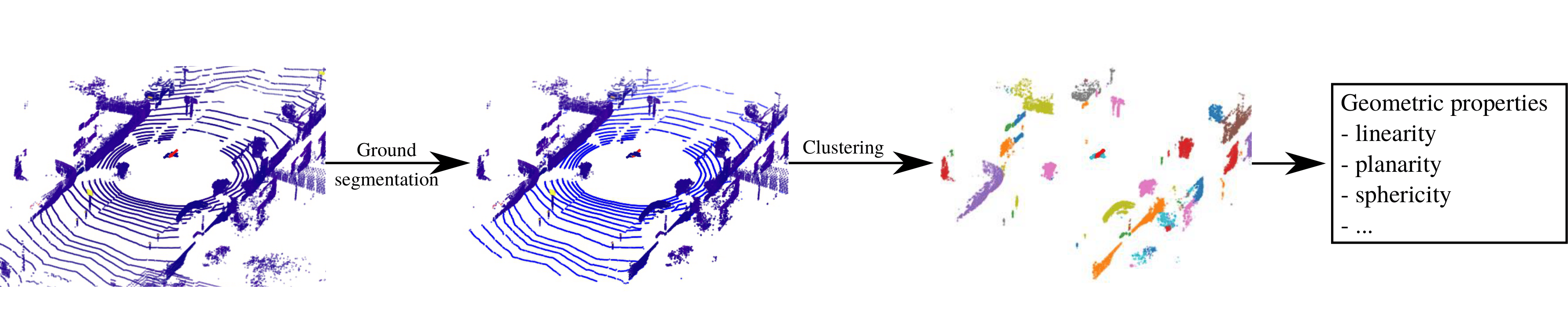
- 👍 Limited data needed
- 👎 Expert tuning
- 👎 Missdetections, false positives (trunks, corners, …)
Machine learning
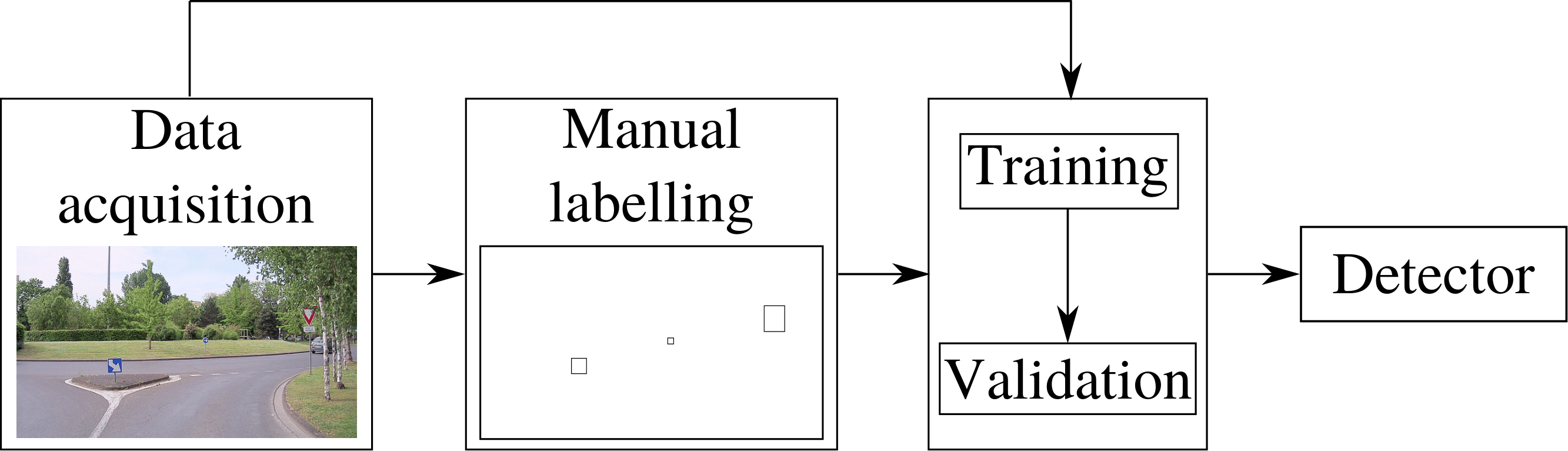
- 👍 Better performance
- 👍 Less tuning, better genericity
- 👎 Huge amount of data needed
- 👎 Labelling
Case study: poles for localization
- Map for localization
- Maximize map usage -> poles common in road environments
- Minimize risks of false detections -> map-specific detection
- Machine learning for detection
- Minimize or avoid human labelling
- Leverage maps for automatic annotation
- Multi-sensor post-processing for automatic annotation
- Training with automatic annotations
- Uncertainty handling
- Minimize or avoid human labelling
- Localization using trained detectors without human input

Multi-modal Automatic Image Annotation
Problem Statement
Multi-modal Automatic Image Annotation
Training with Pointwise Automatic Annotations
Multi-sensor Localization
Conclusion
Map-aided annotation
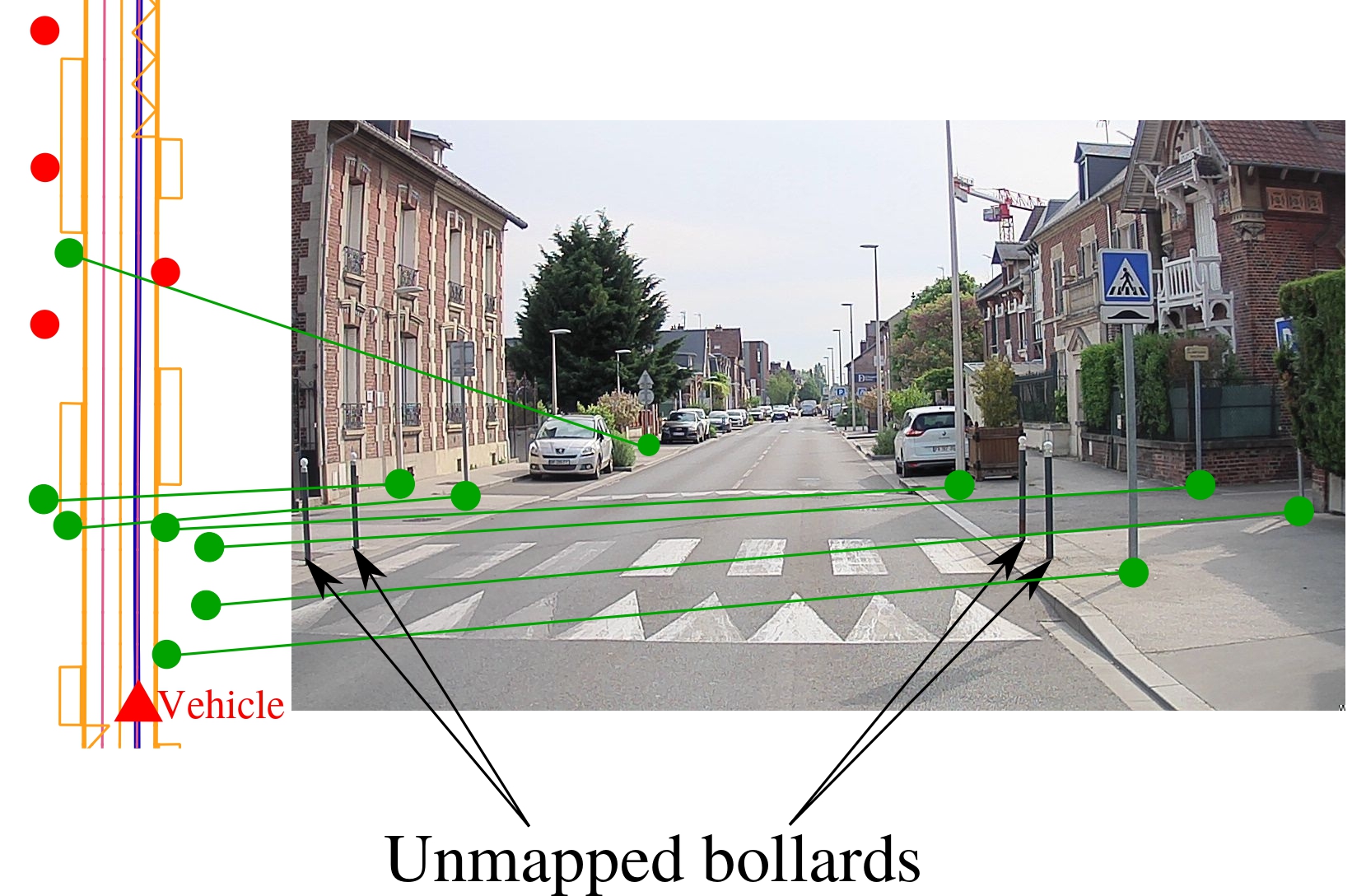
2D map projection with localization reference
 Naive projection
Naive projection
 Projection error source
Projection error source
Lidar refinement
 Ground estimation and annotation projection
Ground estimation and annotation projection
 Occluded pole bases removal
Occluded pole bases removal
Dataset and evaluation metrics
- Multiple sequences around Compiegne
- 2,830 images manually annotated
- 9,017 poles

Map-aided annotation: Results
| Method | Precision (%) | Recall (%) | MAE-x (px) |
|---|---|---|---|
| M | 84.6 | 35.9 | 3.91 |
Multi-modal annotation
Lidar-based annotation
 Initial image
Initial image
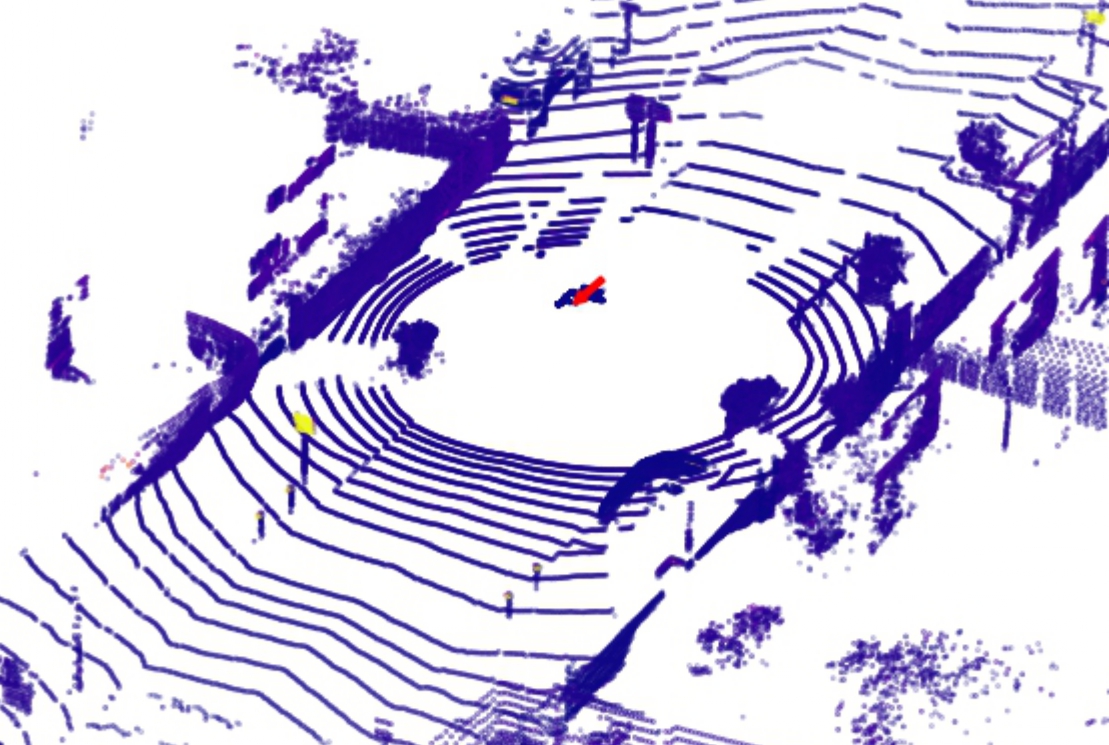 Corresponding point cloud
Corresponding point cloud
Lidar-based annotation
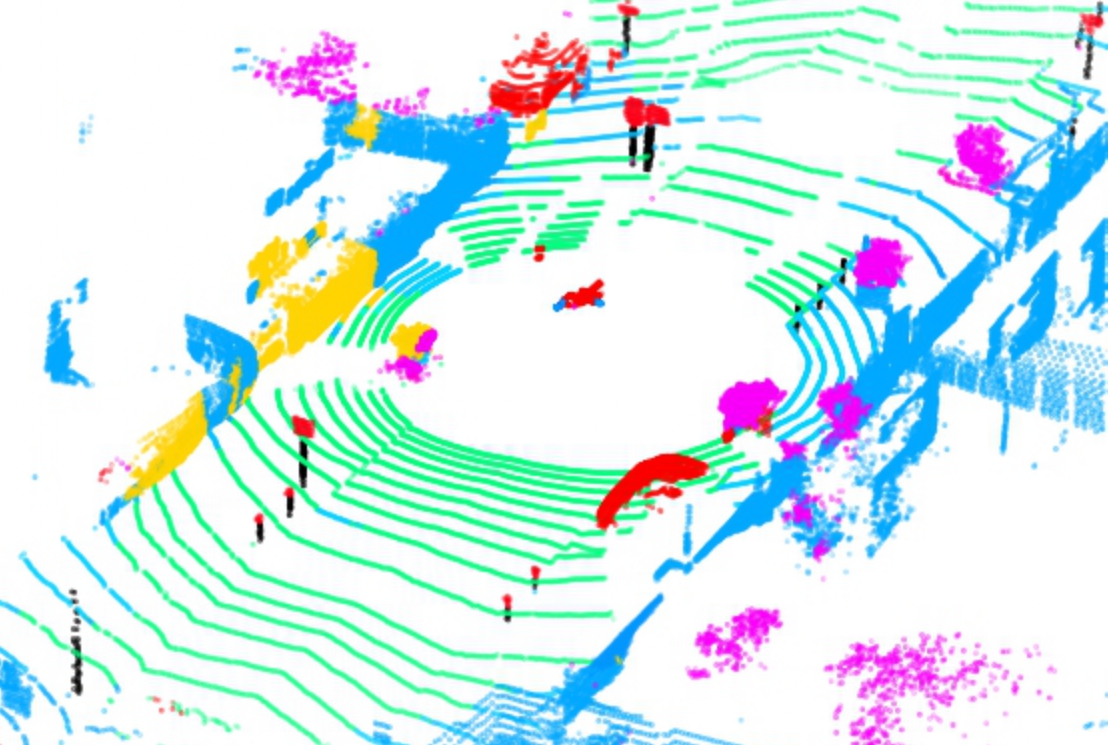 Pointcloud segmentation
Pointcloud segmentation
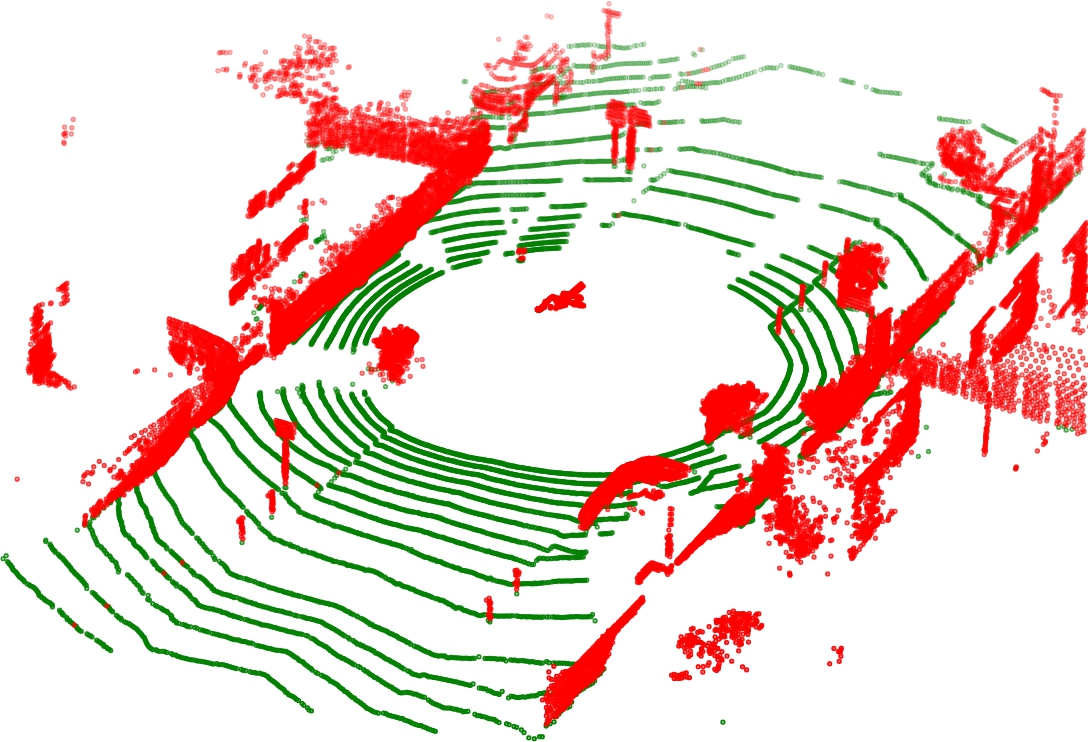 Ground segmentation (more precise)
Ground segmentation (more precise)
X. Zhu et al., “Cylindrical and asymmetrical 3d convolution networks for lidar segmentation”. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021.
Lidar-based annotation: Results
| Method | Precision (%) | Recall (%) | MAE-x (px) |
|---|---|---|---|
| L | 62.6 | 22.7 | 2.63 |
Segmentation-based annotation
 Initial image
Initial image
 Segmentation mask
Segmentation mask
J. Wang et al., “Deep High-Resolution Representation Learning for Visual Recognition,” In IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 10, pp. 3349-3364, 1 Oct. 2021.
Segmentation-based annotation
 Ground mask
Ground mask
 Ground + pole bases mask
Ground + pole bases mask
J. Wang et al., “Deep High-Resolution Representation Learning for Visual Recognition,” In IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 10, pp. 3349-3364, 1 Oct. 2021.
Segmentation-based annotation: Results
| Method | Precision (%) | Recall (%) | MAE-x (px) |
|---|---|---|---|
| S | 40.2 | 80.7 | 1.00 |
Multi-modal annotation results
| Method | Precision (%) | Recall (%) |
|---|---|---|
| M | L | 64.7 | 46.2 |
| M | S | 39.0 | 88.1 |
| M | S | L | 37.7 | 88.7 |
| M & L | 95.7 | 18.8 |
| M & S | 92.5 | 36.6 |
| M & S & L | 99.0 | 17.8 |
Which strategy for optimal learning ?
Training with Pointwise Automatic Annotations
Problem Statement
Multi-modal Automatic Image Annotation
Training with Pointwise Automatic Annotations
Multi-sensor Localization
Conclusion
Pole base detection for cameras
- Pole base detection using object detection
- Based on YOLOv7 network
- Bounding box = visual context
- Automatic annotation: Prone to errors (missed objects, false positives)


Evaluation metrics
- Precision, Recall
- Intersection-over-Union (IoU)
- Average Precision
- Mean horizontal Absolute positioning Error: MAE-x
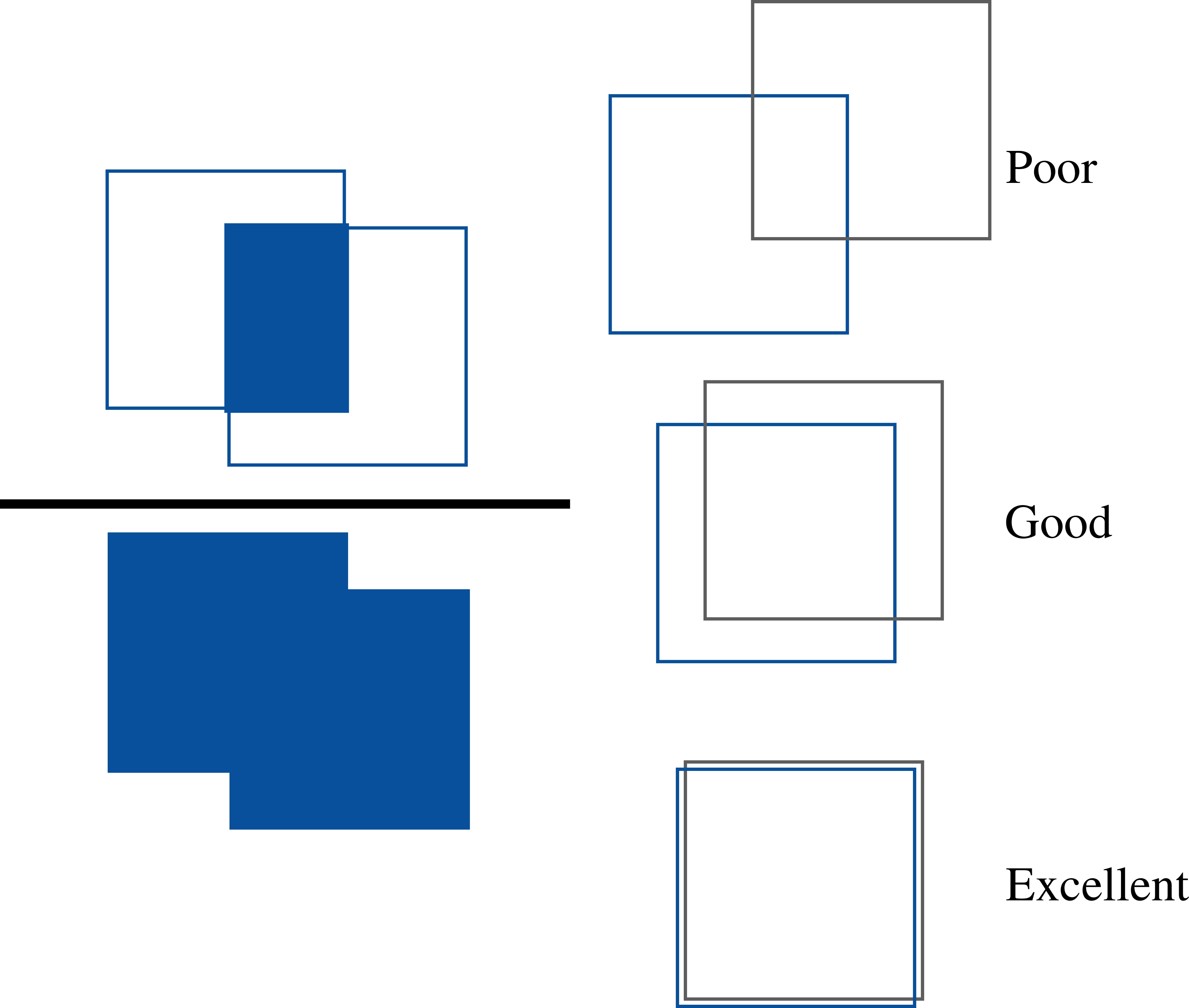
Precision-Recall curve
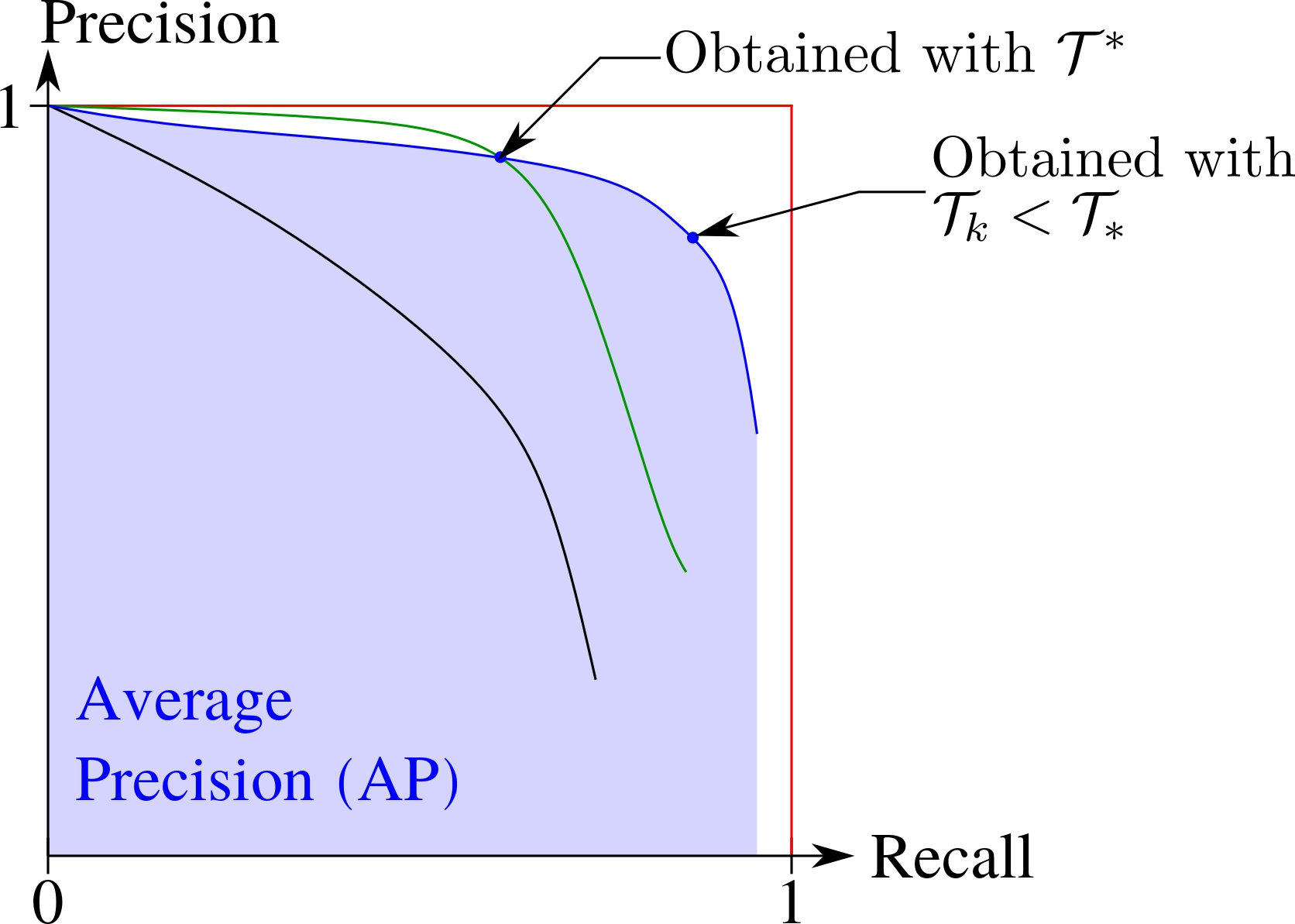
Map-based pole base detection learning
- Training set: 5391 images
- Validation set: 2830 images manually annotated
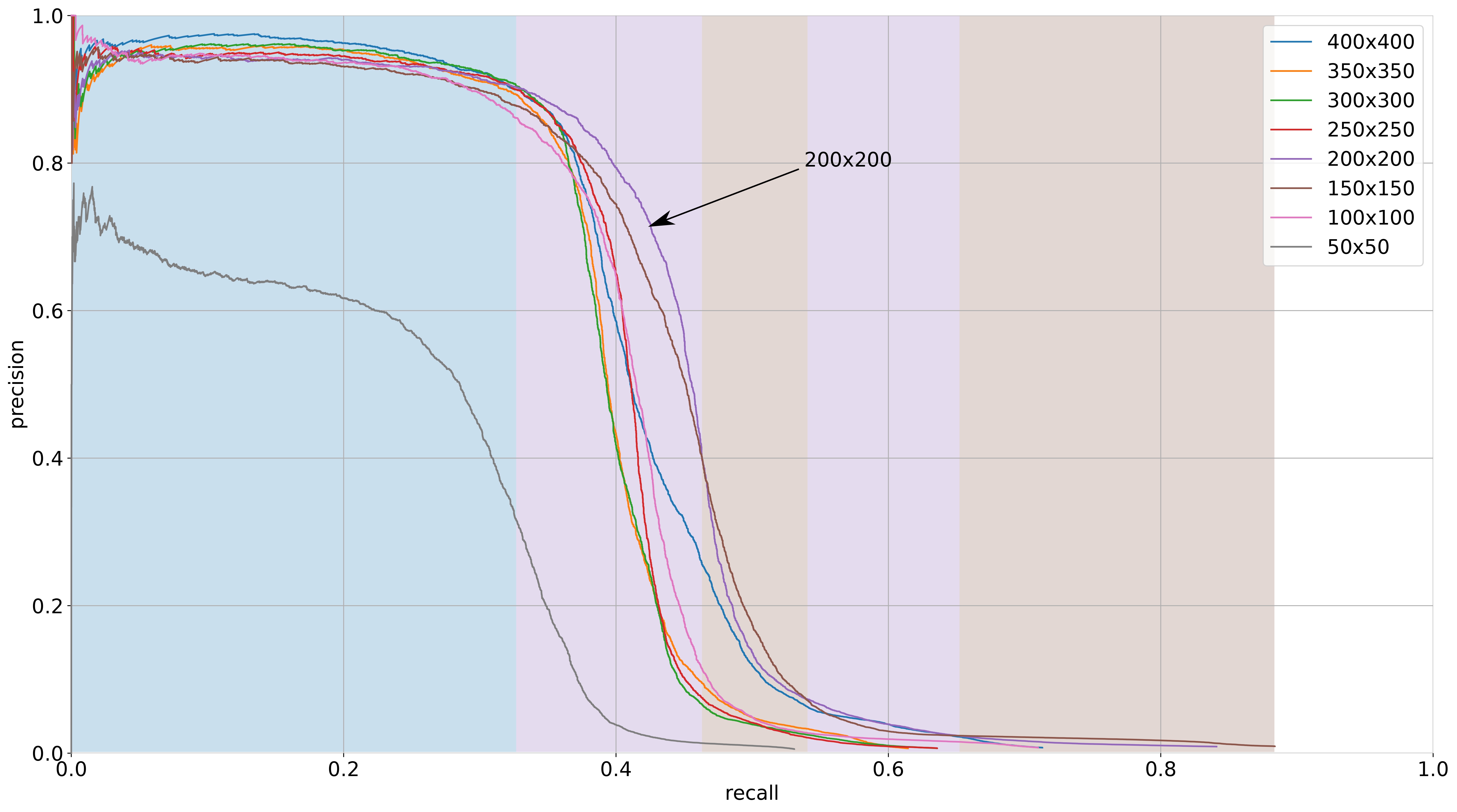
| Box | 50x50 | 100x100 | 150x150 | 200x200 | 250x250 | 300x300 | 350x350 | 400x400 |
|---|---|---|---|---|---|---|---|---|
| AP % | 21.2 | 39.2 | 42.5 | 43.2 | 38.9 | 38.3 | 38.4 | 41.3 |
| MAE-x (px) | 4.01 | 5.84 | 8.90 | 10.84 | 11.76 | 14.97 | 18.2 | 24.30 |
Multi-modal automatic annotation method for learning
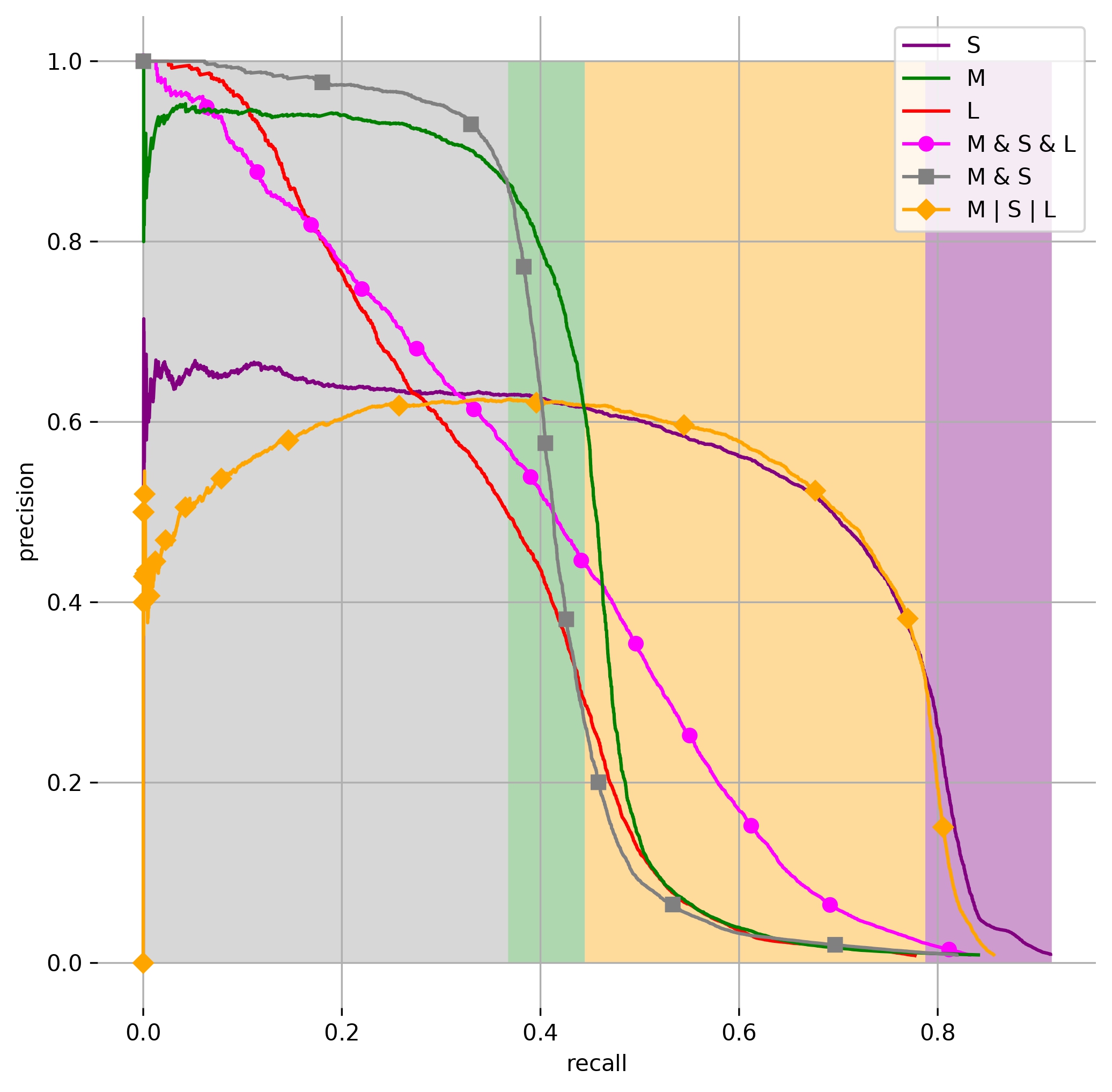
Uncertainty management
- Annotations used for training: Intersection of annotation sets
- Ambiguous cases: Union of annotation sets

Learning with uncertainty management
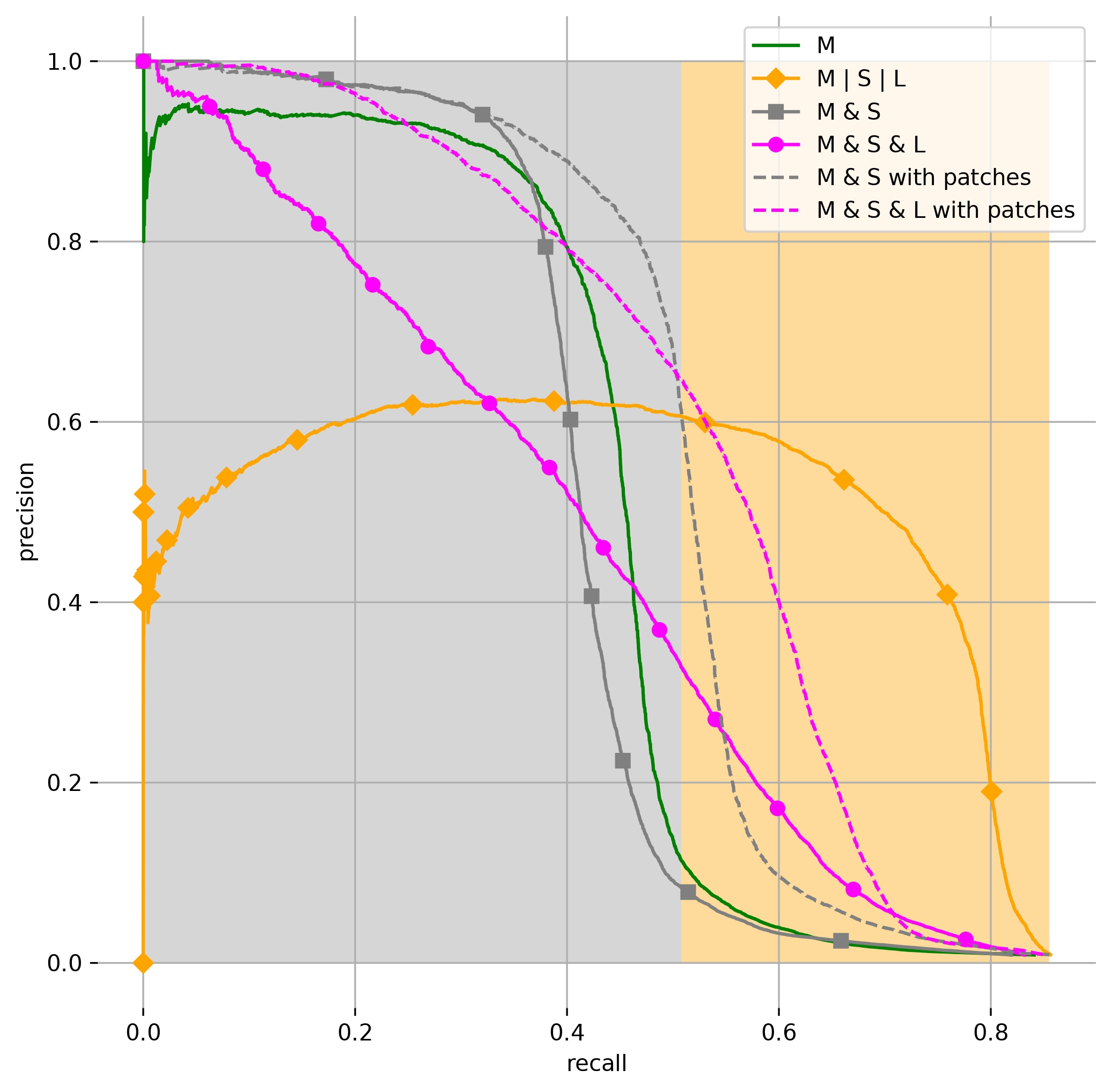
Detection results
- 200x200 box size
- M & S with black patches: Precision 90%, Recall 38,5%
Multi-sensor Localization
Problem Statement
Multi-modal Automatic Image Annotation
Training with Pointwise Automatic Annotations
Multi-sensor Localization
Conclusion
Available detectors
.jpg)
.jpg)
.jpg)
- Integration to a GNSS + Dead Reckoning sensors system
- Combinations: F and All
| Model | M95 | MS95 | M90 | MS90 |
|---|---|---|---|---|
| Precision (%) | 95 | 95 | 90 | 90 |
| Recall (%) | 4.3 | 30.4 | 33.3 | 38.5 |
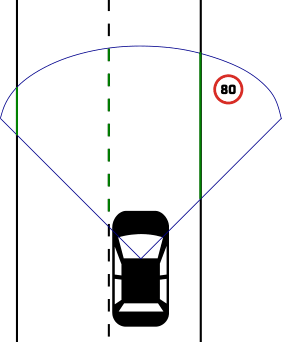
Pole-based localization
- Camera observations
- Lack of depth → map features projected into camera frame
- Use angles for observations and map features in camera frame
- Pose and calibration errors impact
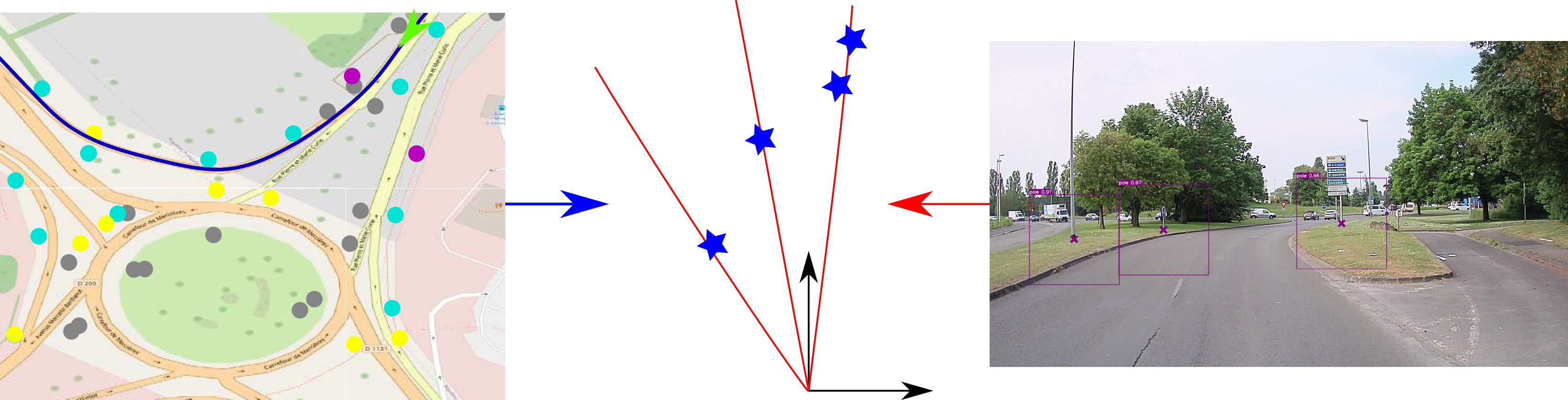
Data association
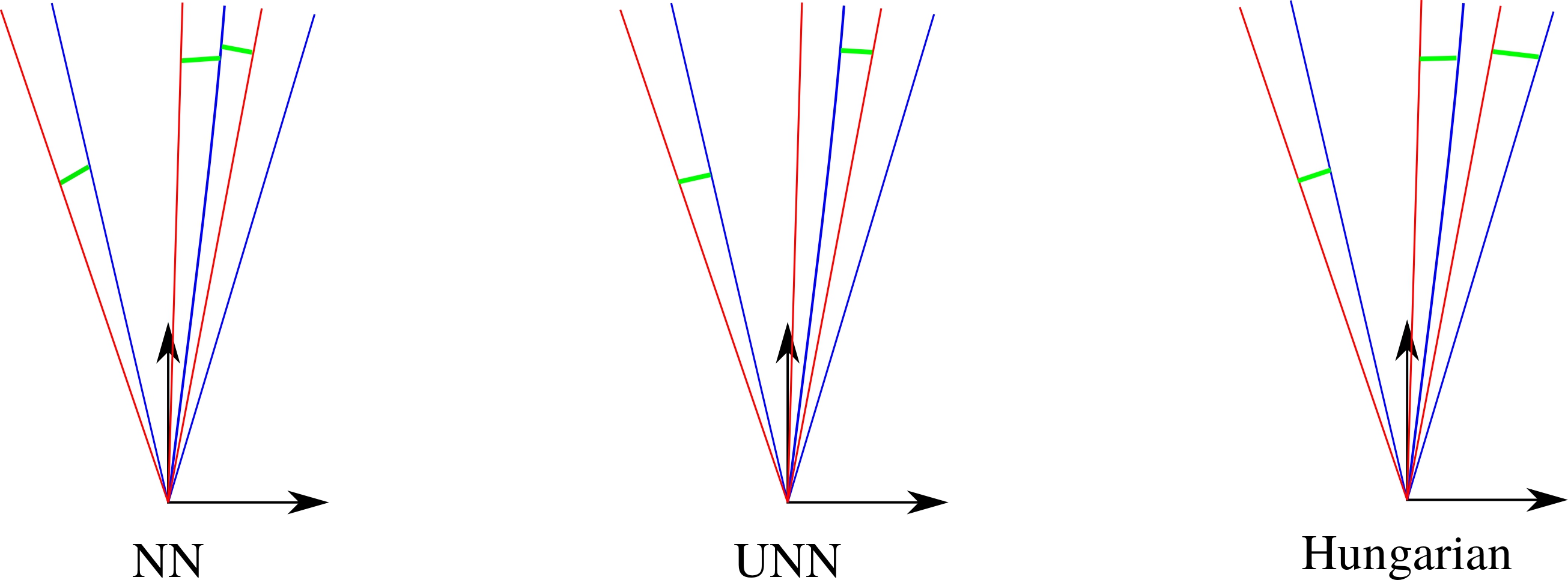
- Avoid wrong associations: gating
- Hungarian chosen
Nominal scenario
- Extended Kalman Filter
- Dead reckoning: 4-wheel speed + yaw rate model
- GNSS: SPP pose estimation
- Tightly-coupled cameras
- 50Hz pose estimation frequency
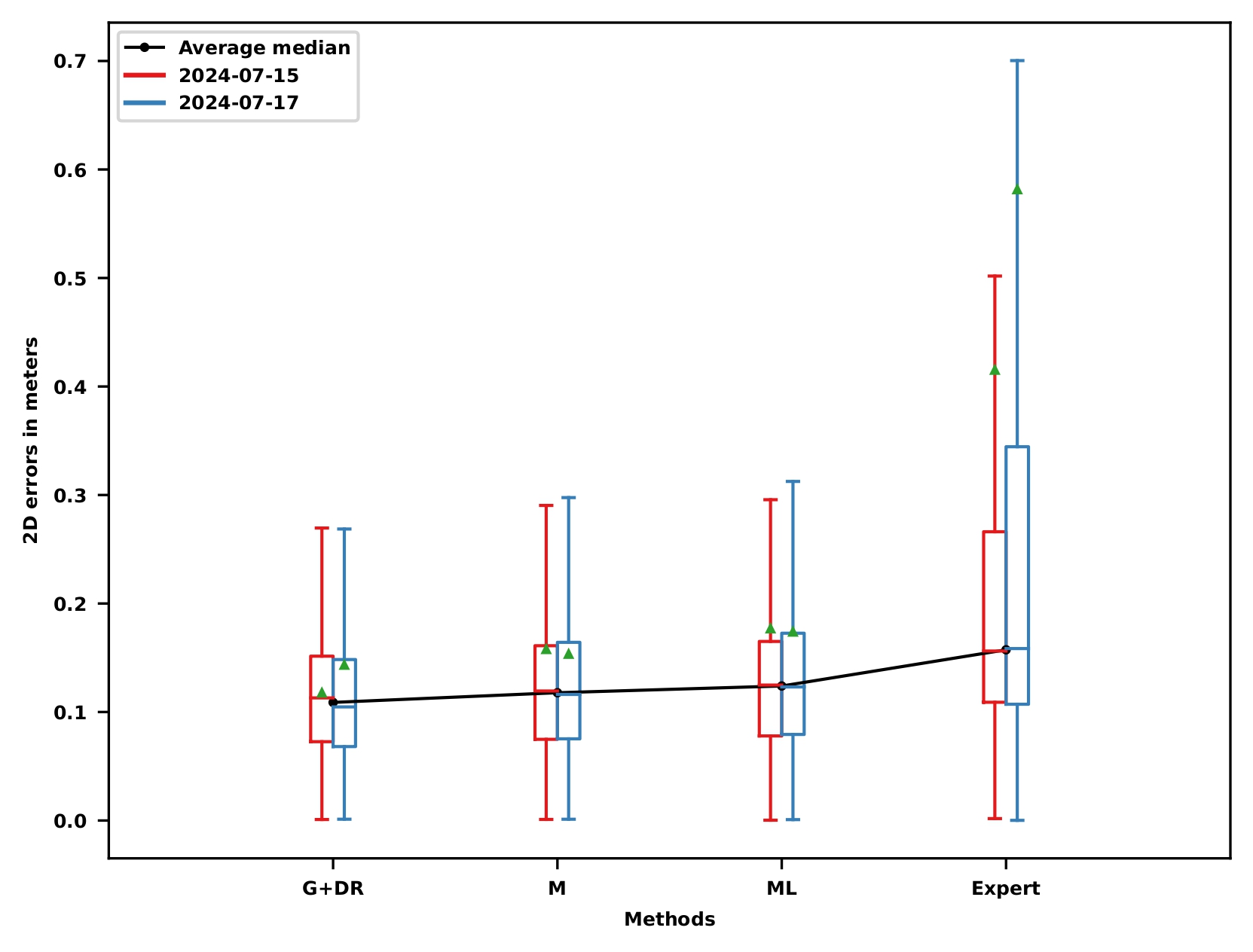
Localization results
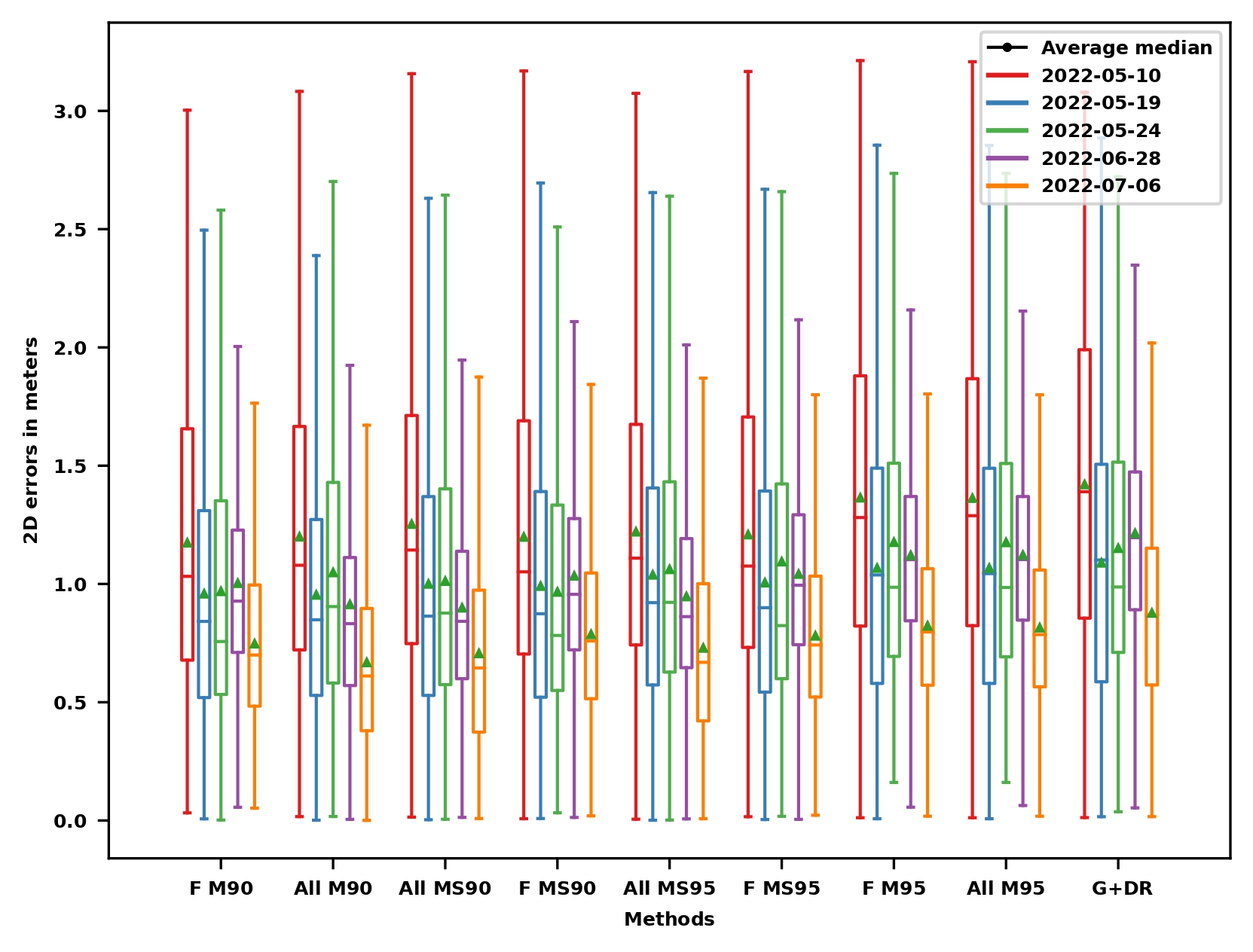
Localization results
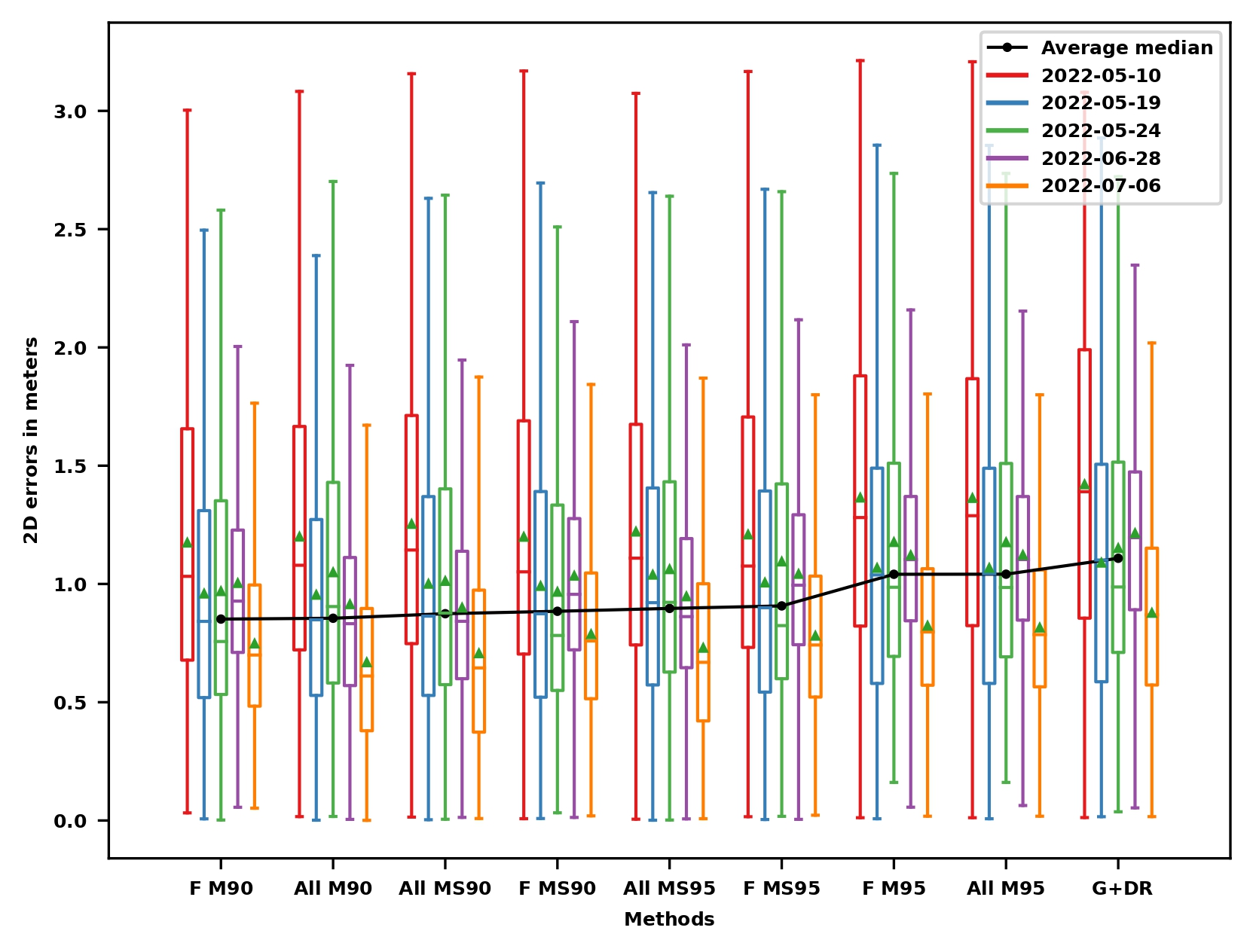
Localization results
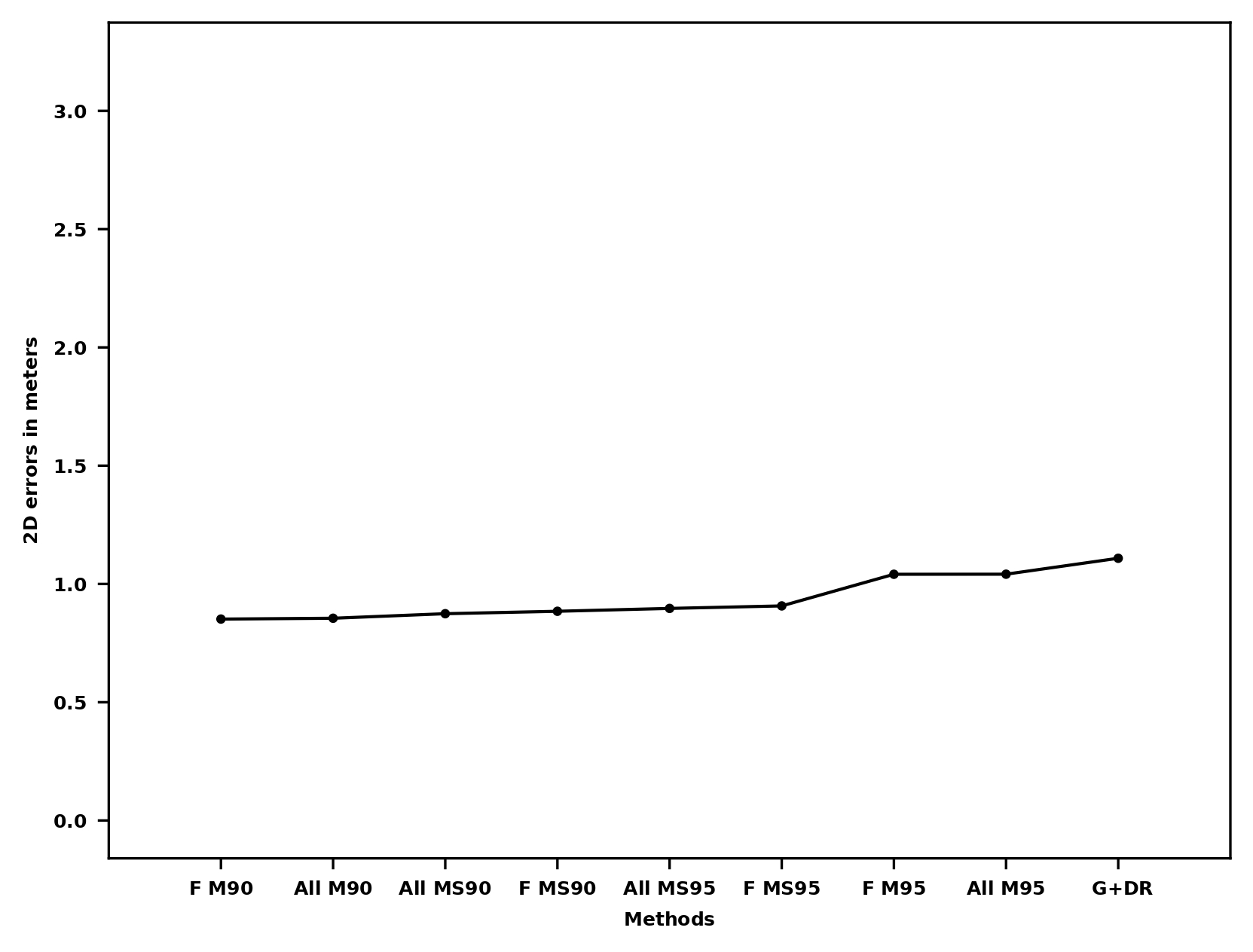
Performance limitations
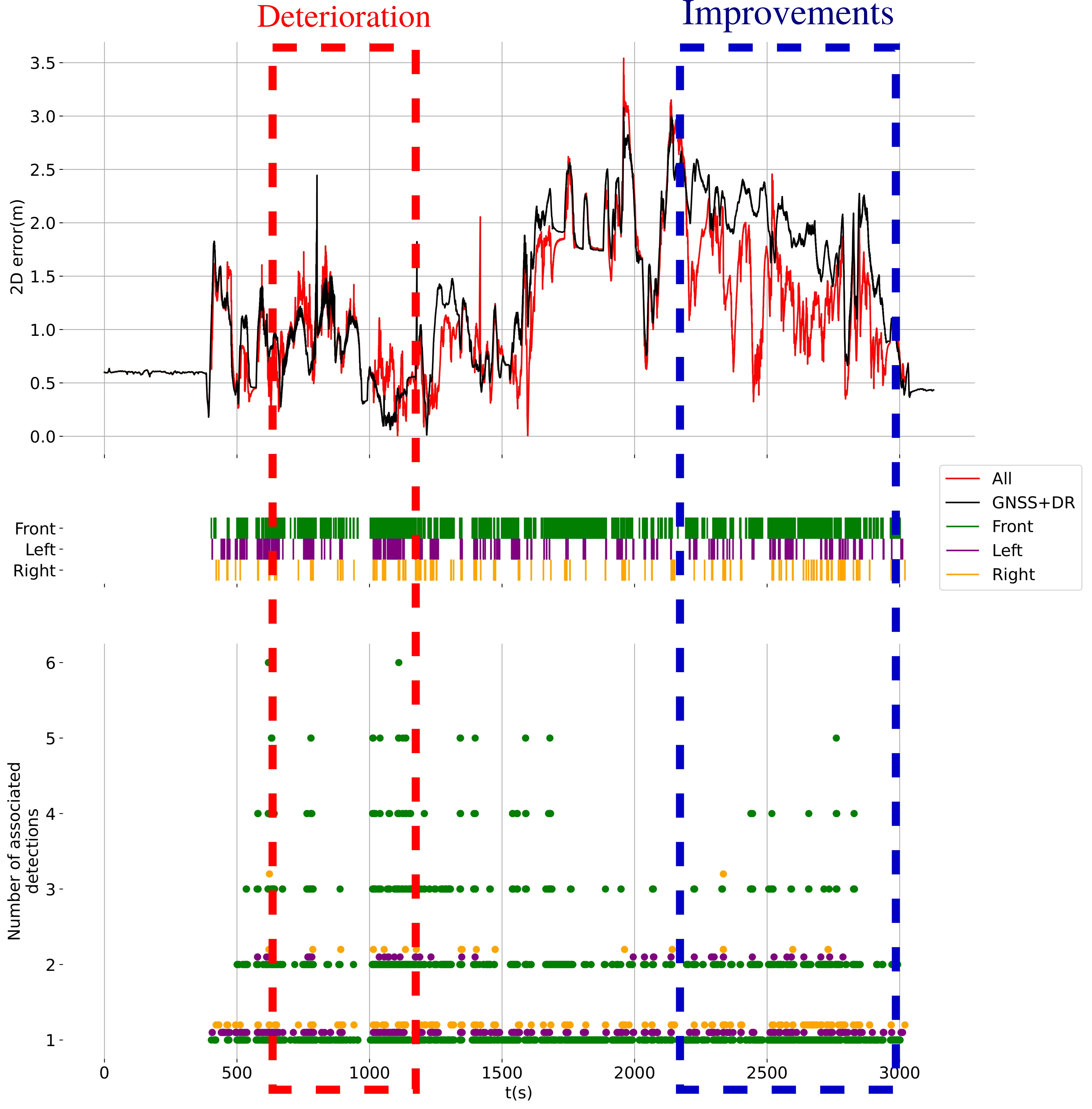

Better prior pose for data association improvements
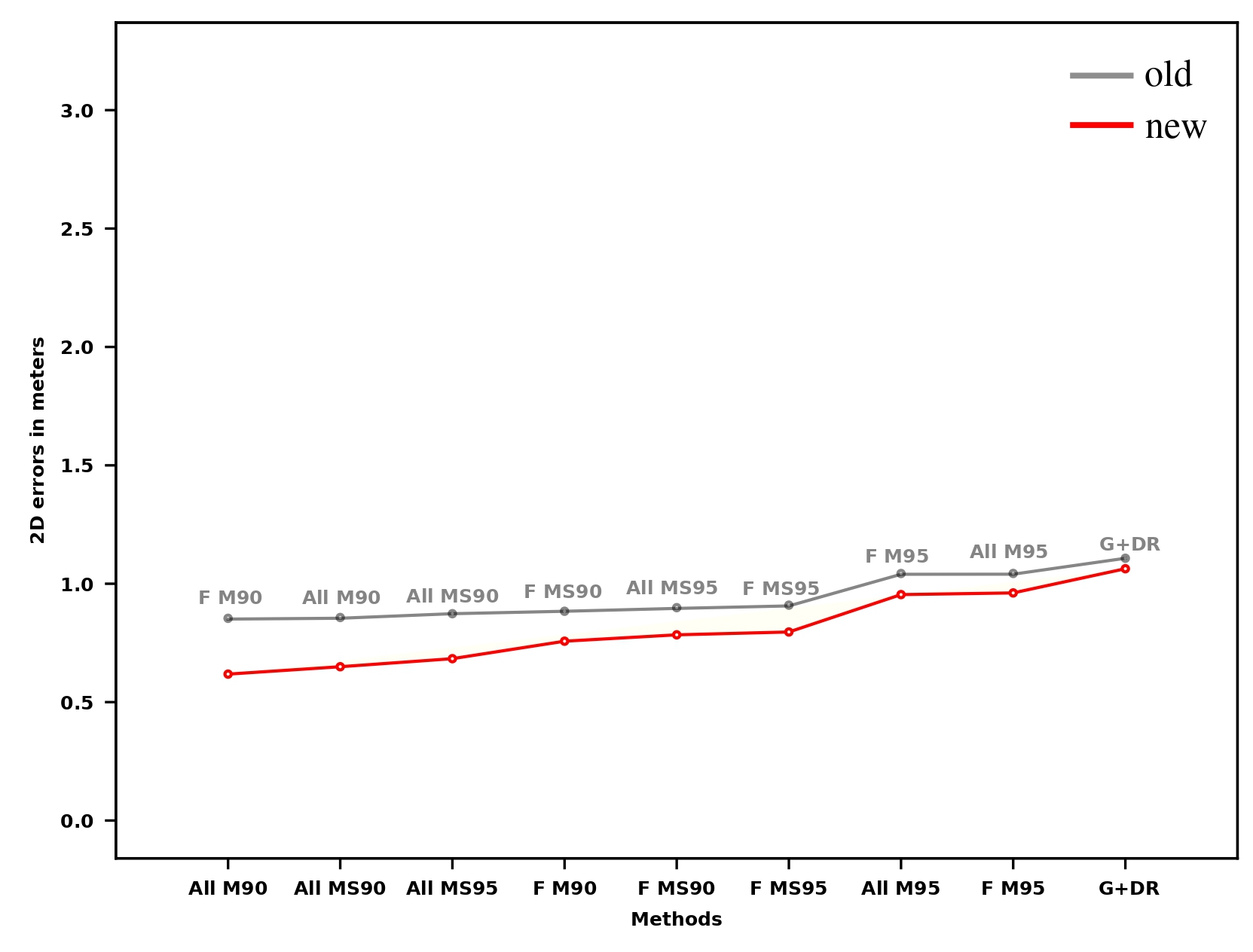
Conclusion
Problem Statement
Multi-modal Automatic Image Annotation
Training with Pointwise Automatic Annotations
Multi-sensor Localization
Conclusion
Conclusion
- HD Vector Maps: prior for annotation and localization. Map-specific detectors.
- Multi-Modal Annotation: No human cost, infinite data.
- Genericity: Adaptation for any sensor. Proof-of-concept with lidars in the manuscript.
- Key Limitations: Errors in maps, data association challenges, high costs for large-scale maps, and lack of detailed visual description.
Perspectives
- Automatic annotation : Additional sources, other landmarks, semantics, uncertainty.
- Pole detection : Annotation uncertainty, model alternatives, robustness to variations.
- Localization: Integrity, data association.
- General: Map correction, calibration.
Associated Publications
- Missaoui, Benjamin, Maxime Noizet, and Philippe Xu “Map-aided annotation for pole base detection”. In: IV23. Anchorage, Alaska, USA.
- Maxime Noizet, Philippe Xu, and Philippe Bonnifait “Pole-Based Vehicle Localization With Vector Maps: A Camera-LiDAR Comparative Study”. In: ITSC23, Bilbao, Spain.
- Maxime Noizet, Philippe Xu, and Philippe Bonnifait “Automatic Image Annotation for Mapped Features Detection”. In: IROS24, Abu Dhabi, United Arab Emirates.
- Vilalta Estrada, Laia, Cristina Munoz Garcia, Enrique Dominguez Tijero, Maxime Noizet, Philippe Xu, Su Yin Voon, Stan Guerassimov, and Wesley W. Cox. “ERASMO – Enhanced Receiver for AutonomouS MObility”. In: 15th ITS European Congress. 2023. Lisbon, Portugal.
- Ph. Xu, M. Noizet, L. Vilalta Estrada, J. Ibañez-Guzmán, E. Starwiarski, P. Nemry, S. Y. Voon, W. Fox and K. Callewaert. High integrity navigation for intelligent vehicles. In International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+), Denver, Colorado, USA, September 11-15, 2023.
Thank you for your attention !
Appendices
Learning on manually annotated data
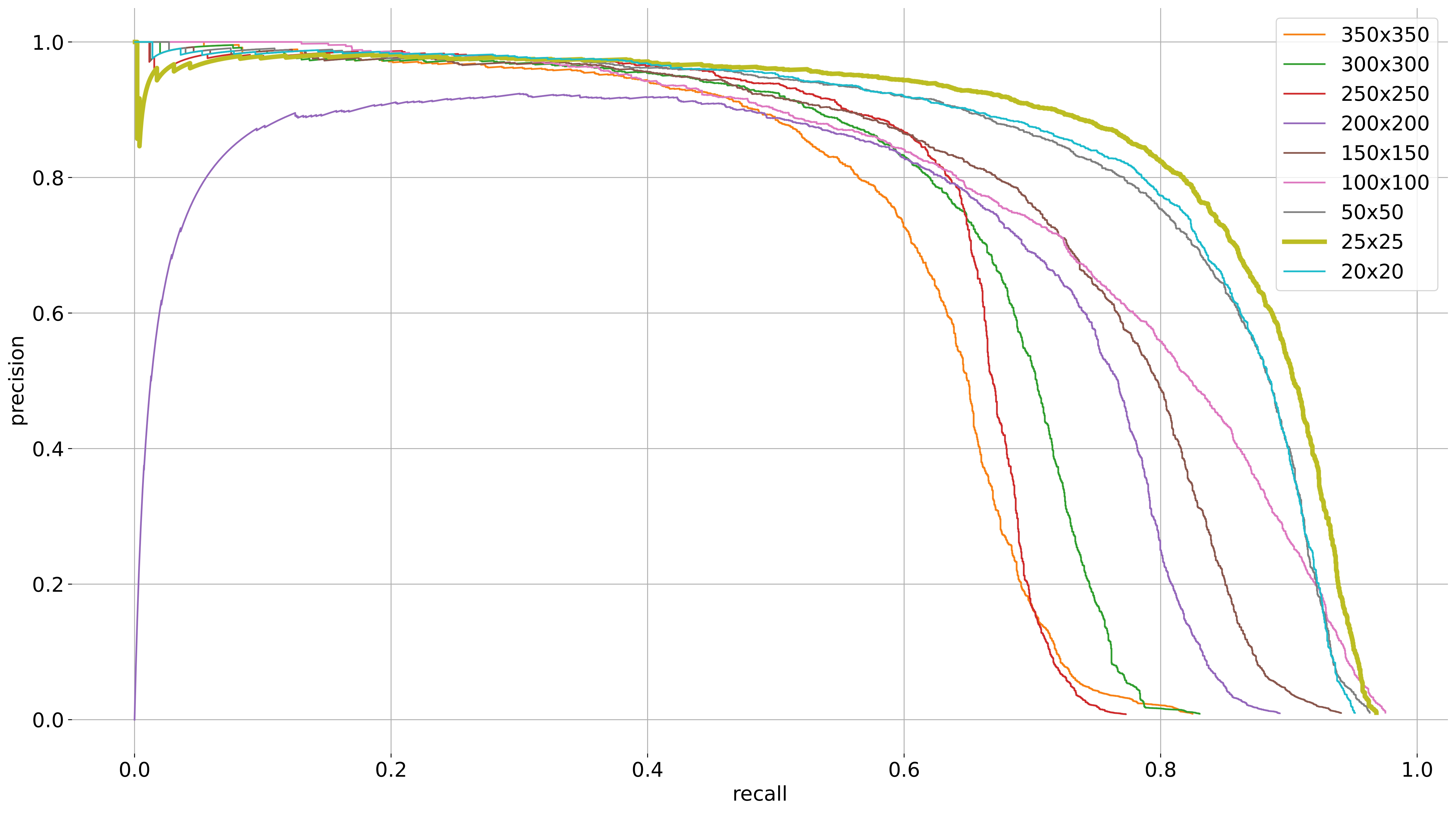
- Higher recall reachable
- Optimal box size: 25x25
Appendices
Kalman filter
Vehicle state: \(\boldsymbol{x}_{k} = \left[x_{B,k}, y_{B,k}, \theta_{B,k}, v_{k}, \dot{\theta}_{k} \right]^{\top}\) + Constant velocity evolution model
GNSS observations
\[\begin{align} \boldsymbol{z}^{\text{G}}_k = \begin{bmatrix} x_{B,k} \\ y_{B,k} \\ \theta_{B,k} \end{bmatrix} + \begin{bmatrix} \cos\theta_{B,k} & -\sin\theta_{B,k} & 0 \\ \sin\theta_{B,k} & \cos\theta_{B,k} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} t_x\\ t_y \\ 1 \end{bmatrix} + \boldsymbol{\beta}^\text{G}_k \end{align}\]
- Wheel speeds
\[\begin{equation} \left\{\begin{aligned} \boldsymbol{z}^{\text{W}_{rl}}_k &= \frac{2\pi}{\rho_{rl}}\left(v_k - \frac{\ell_r}{2}\dot{\theta}_k \right) + \boldsymbol{\beta}^{\text{W}_{rl}}_k\\ \boldsymbol{z}^{\text{W}_{rr}}_k &= \frac{2\pi}{\rho_{rr}}\left(v_k + \frac{\ell_r}{2}\dot{\theta}_k \right) + \boldsymbol{\beta}^{\text{W}_{rr}}_k \\ \boldsymbol{z}^{\text{W}_{fl}}_k &= \frac{2\pi}{\rho_{fl}} \sqrt{\ell_{rf}^2\dot{\theta}_k^2 + \left(v_k - \frac{\ell_f}{2} \dot{\theta}_k\right)^2} + \boldsymbol{\beta}^{\text{W}_{fl}}_k \\ \boldsymbol{z}^{\text{W}_{fr}}_k &= \frac{2\pi}{\rho_{fr}} \sqrt{\ell_{rf}^2\dot{\theta}_k^2 + \left(v_k + \frac{\ell_f}{2} \dot{\theta}_k\right)^2} + \boldsymbol{\beta}^{\text{W}_{fr}}_k \end{aligned}\right. \end{equation}\]
- yaw rate \(\boldsymbol{z}^{\text{Y}}_k = \dot{\theta}_k + \boldsymbol{\beta}^{\text{Y}}_k\)
Kalman filter: Camera measurements
- Detections
\[\begin{align} {}^{\text{C}} \boldsymbol{Y}^{\alpha}_k = \left\{\left. {}^{\text{C}}\boldsymbol{y}^{\alpha}_{k,i}=\alpha_{k,i}\in\left[-\pi;\pi\right)\right| i=1,\ldots \right\} \end{align}\] \[\begin{align} \alpha_{k,i} = atan\left(\frac{u_{k,i} - c_x}{f_x}\right) \end{align}\]
- Projected map
\[\begin{align} {}^{\text{C}} \boldsymbol{\mathcal{M}}^{\alpha}_k=\left\{\left.{}^{\text{C}}\boldsymbol{m}^{\alpha}_{k,j}=\alpha_{k,j}\in\left[-\pi;\pi\right)\right|j=1,\ldots \right\} \end{align}\]
- Chosen distance for hungarian method
\[\begin{align} \mathcal{D}^\text{C}_{k,i,j} = \left( {}^{\text{C}} \boldsymbol{y}^{\alpha}_{k,i} - {}^{\text{C}}\boldsymbol{m}^{\alpha}_{k,j}\right)^2 \end{align}\]
- Observation model
\[\begin{equation} {}^{\text{C}} \boldsymbol{y}^{\alpha}_{k,i} = {}^{\text{C}}\boldsymbol{m}^{\alpha}_{k,j} + \boldsymbol{\beta}^\alpha_{k,i} \end{equation}\]
Kalman filter: Covariances
| Covariance | |
|---|---|
| Evolution model | \(\left[10^{-2}, 10^{-2}, 10^{-2}, 10^2, 10^{-1}\right] \cdot \mathbb{I}_{5}\) |
| Wheel speeds | \(0.273^{2} \cdot \mathbb{I}_{4}\) |
| Yaw rate | \(10^{-12}\) |
| Bearings | \(4 \cdot 10^{-4}\) |
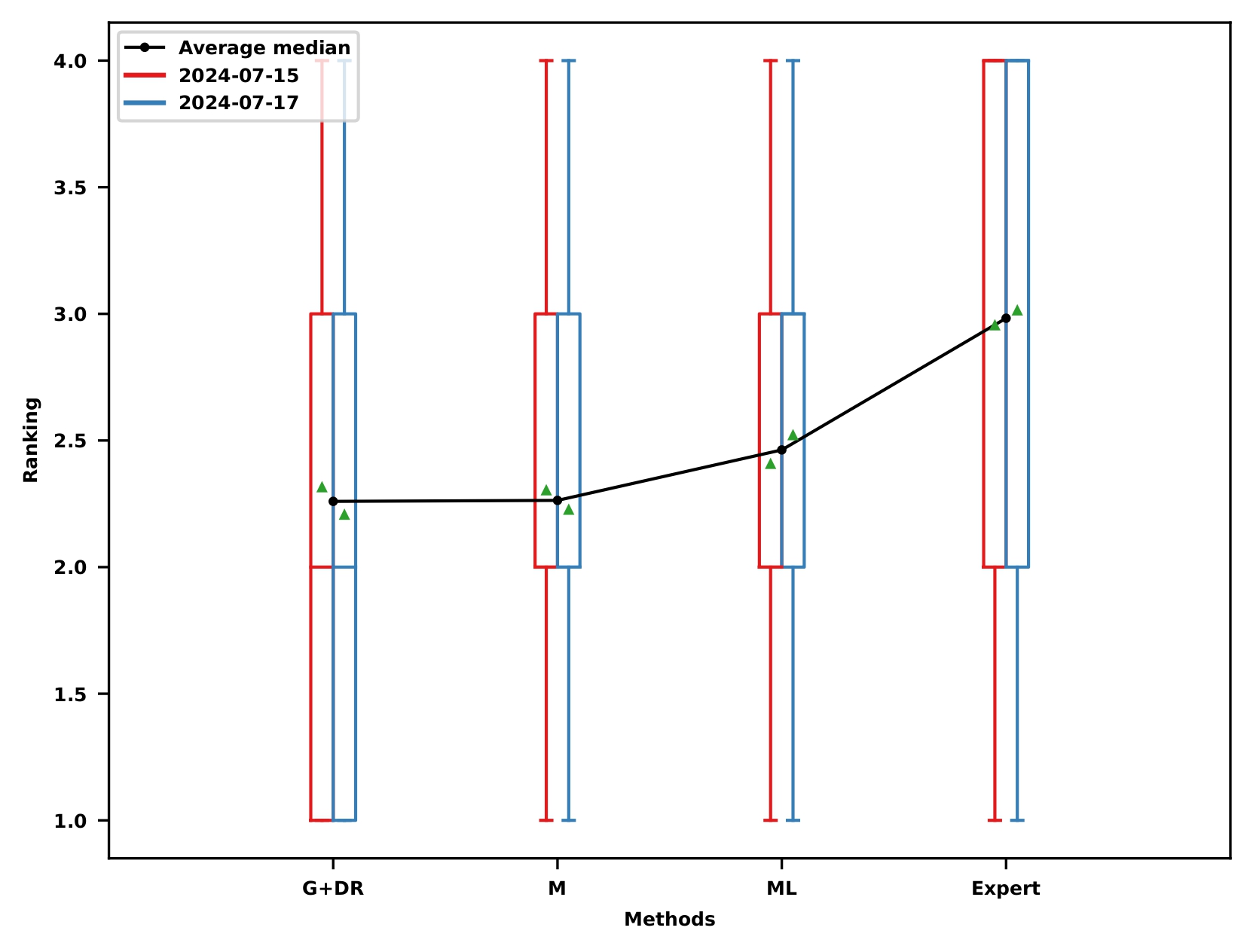
Localization results: Ranking
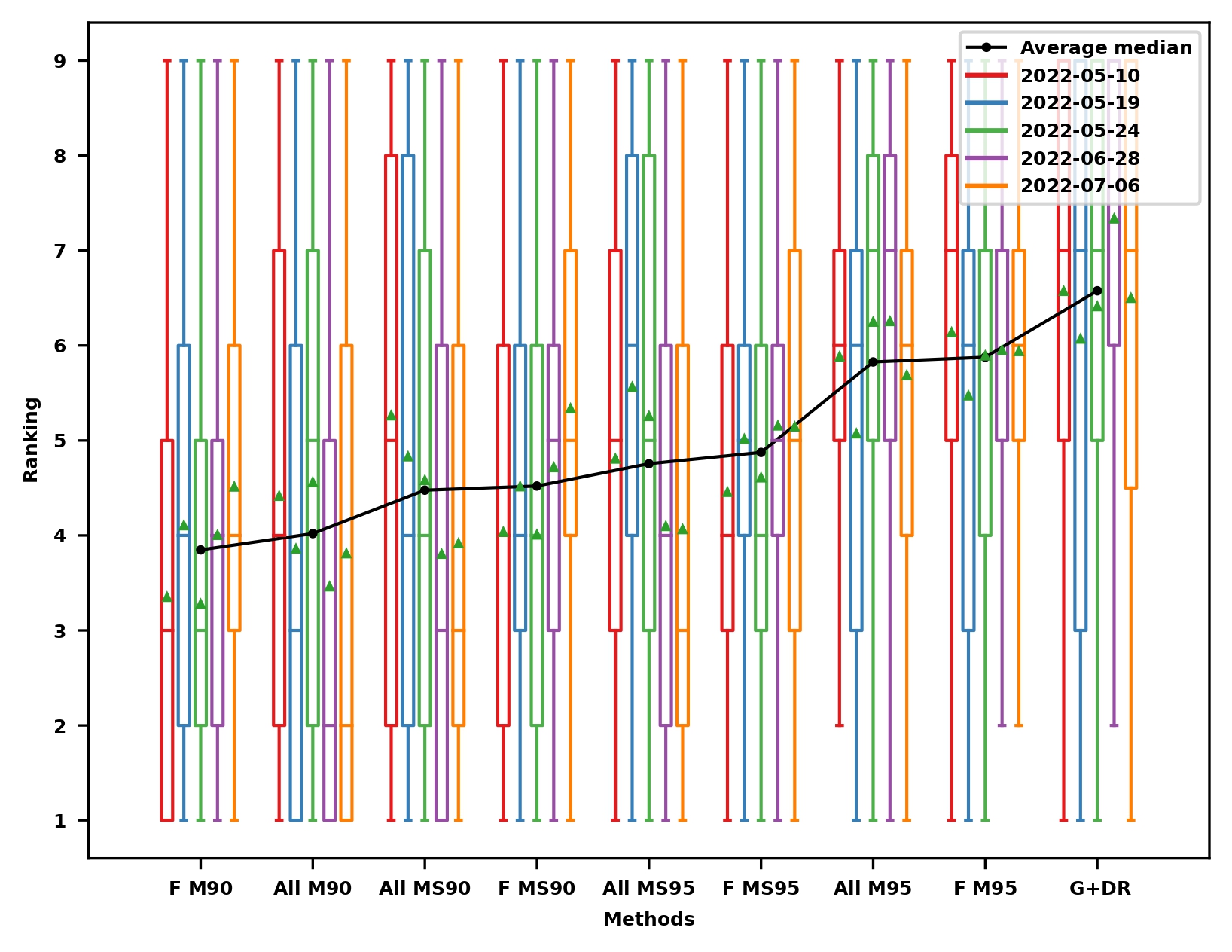
Localization reference for data association: Ranking
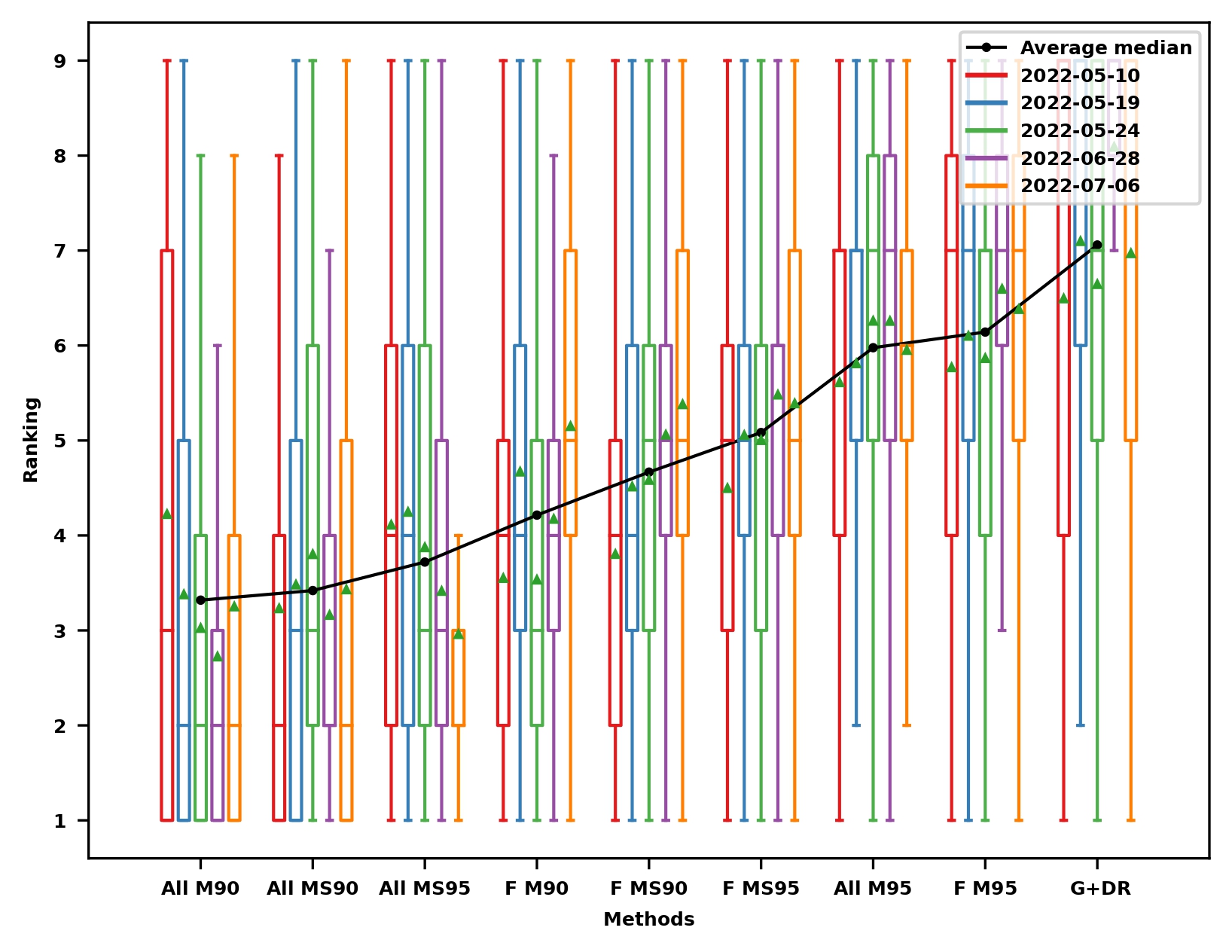
Results with PPP-RTK
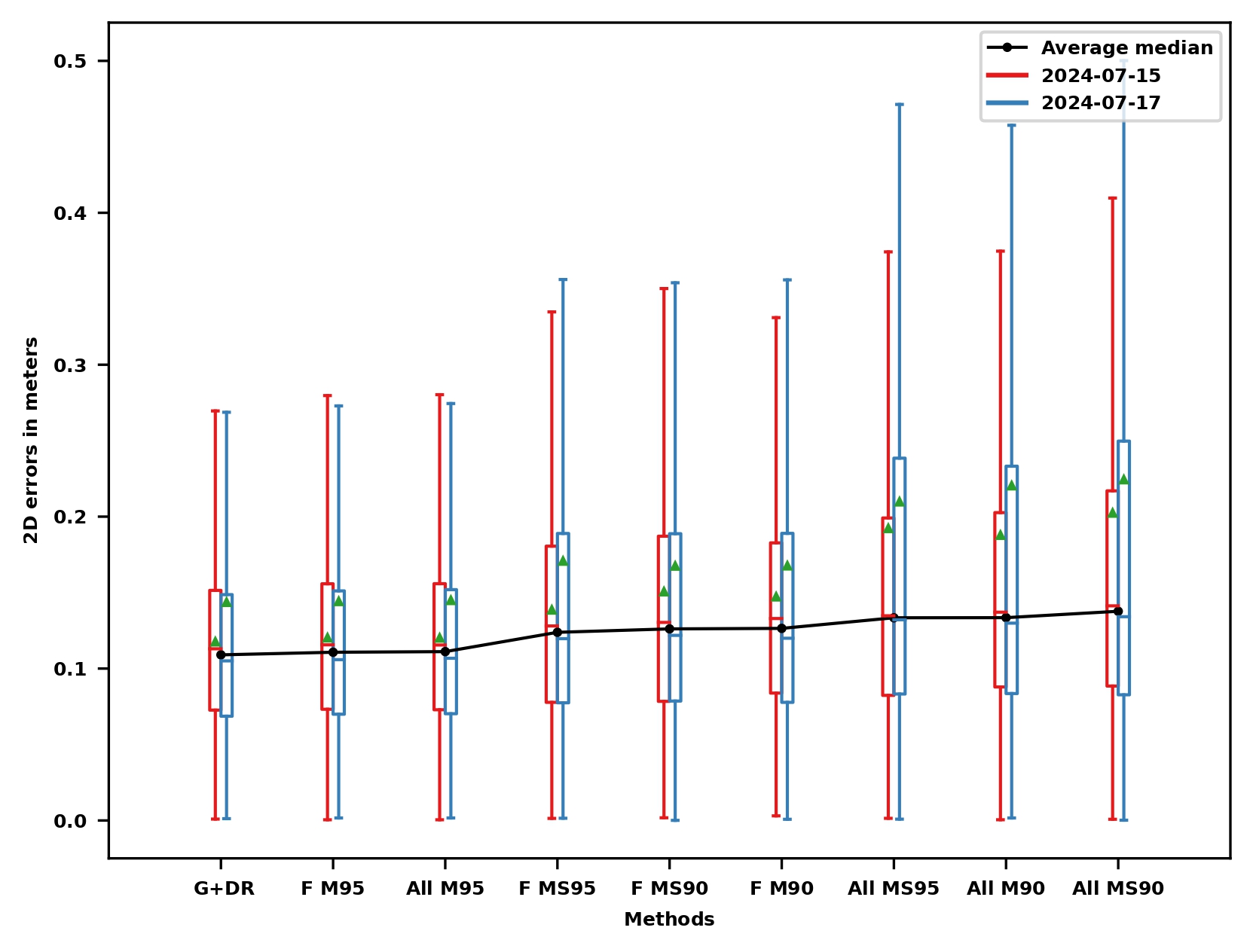
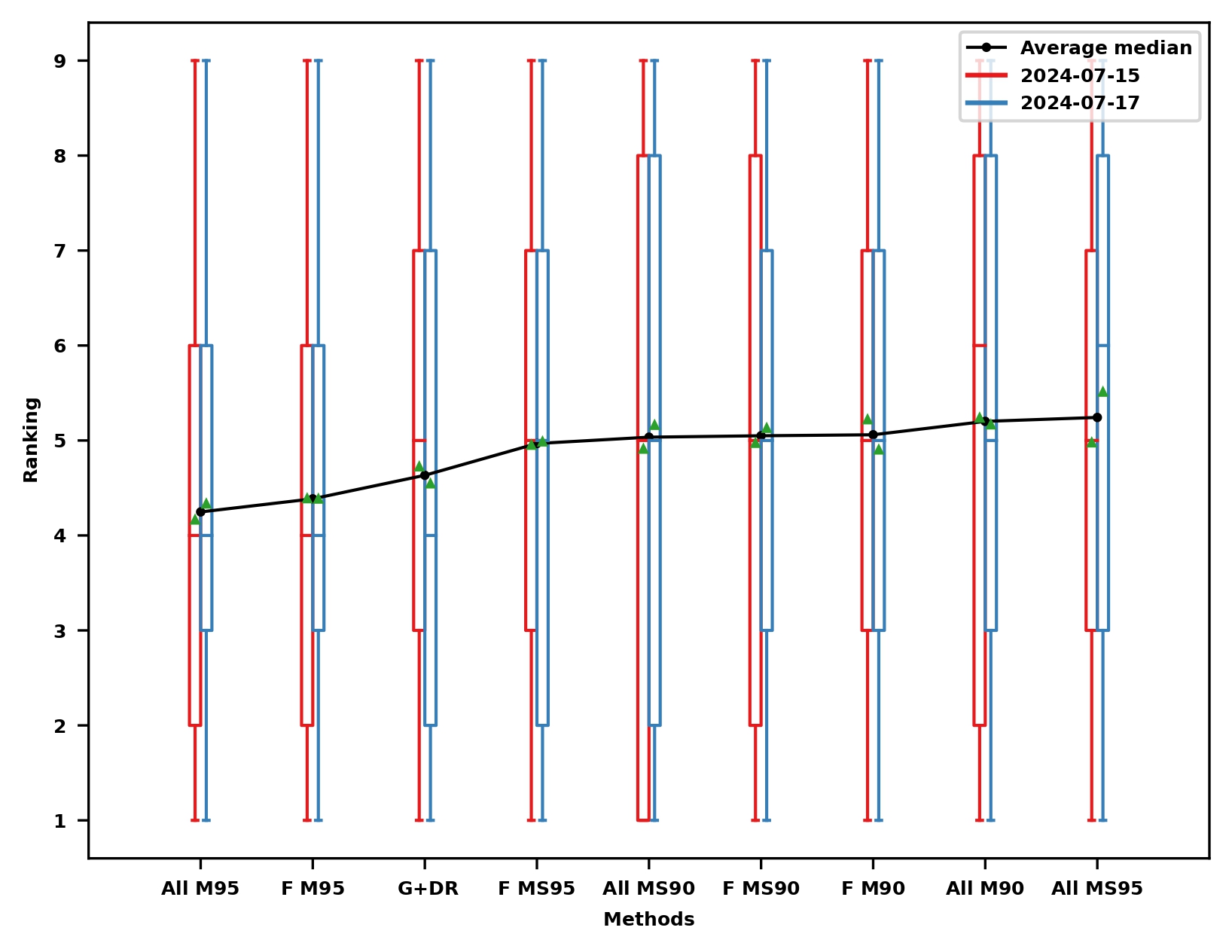
Appendices
Lidar: Map-based annotation

- Data association between map points and clusters
Lidar: Lidar-based annotation
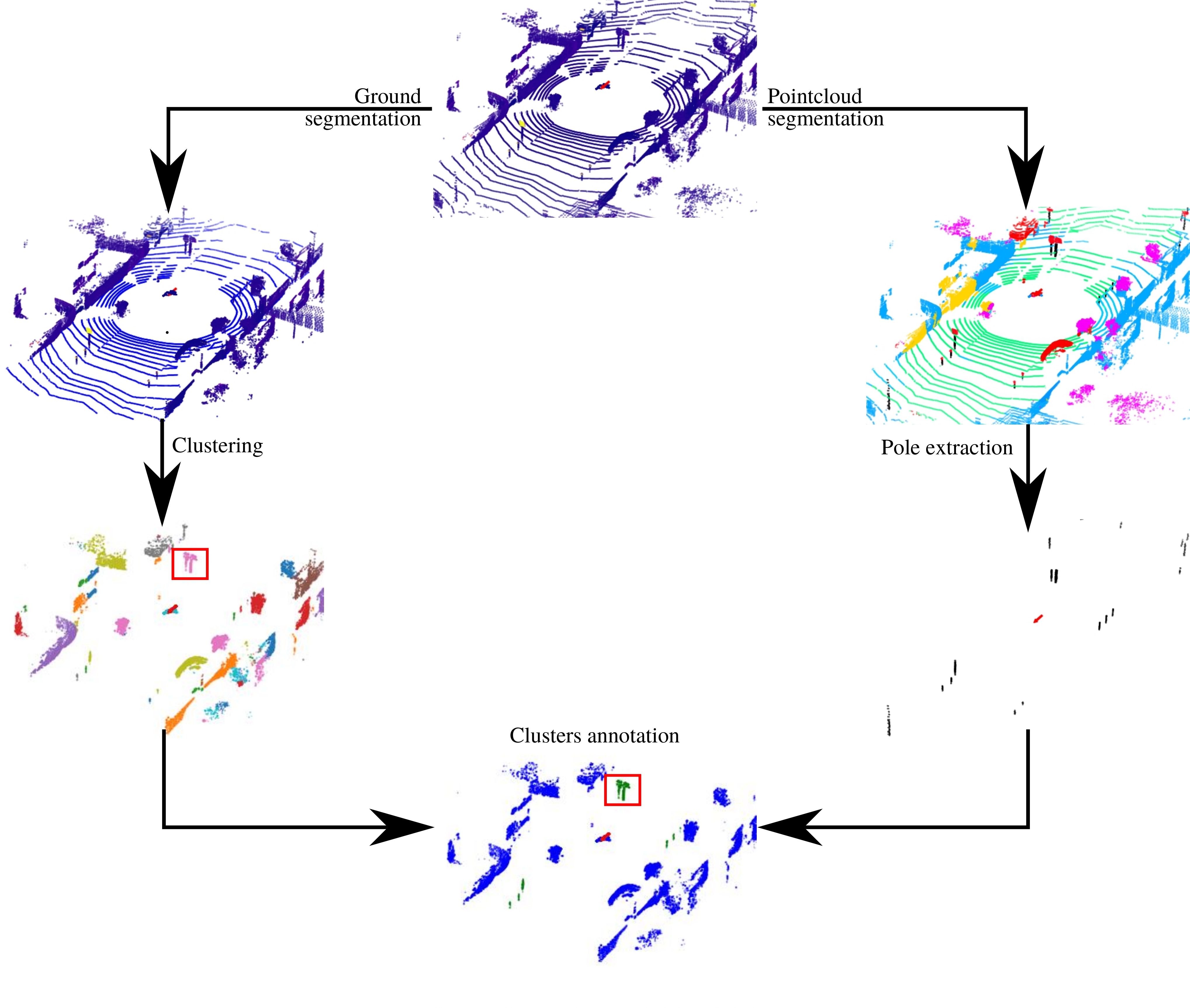
Lidar: Principal Component Analysis (PCA)
Points \[ X = \begin{pmatrix} x_0 & x_1 & \dots & x_N \\ y_0 & y_1 & \dots & y_N \end{pmatrix} \]
Mean
\[ \bar{X} = \begin{pmatrix} \bar{x} \\ \bar{y} \end{pmatrix} \]
Lidar: PCA - Covariance matrix
\[ Cov = \frac{ \left(X - \bar{X}\right) \cdot \left( X - \bar{X} \right)^T }{ N - 1 } \]
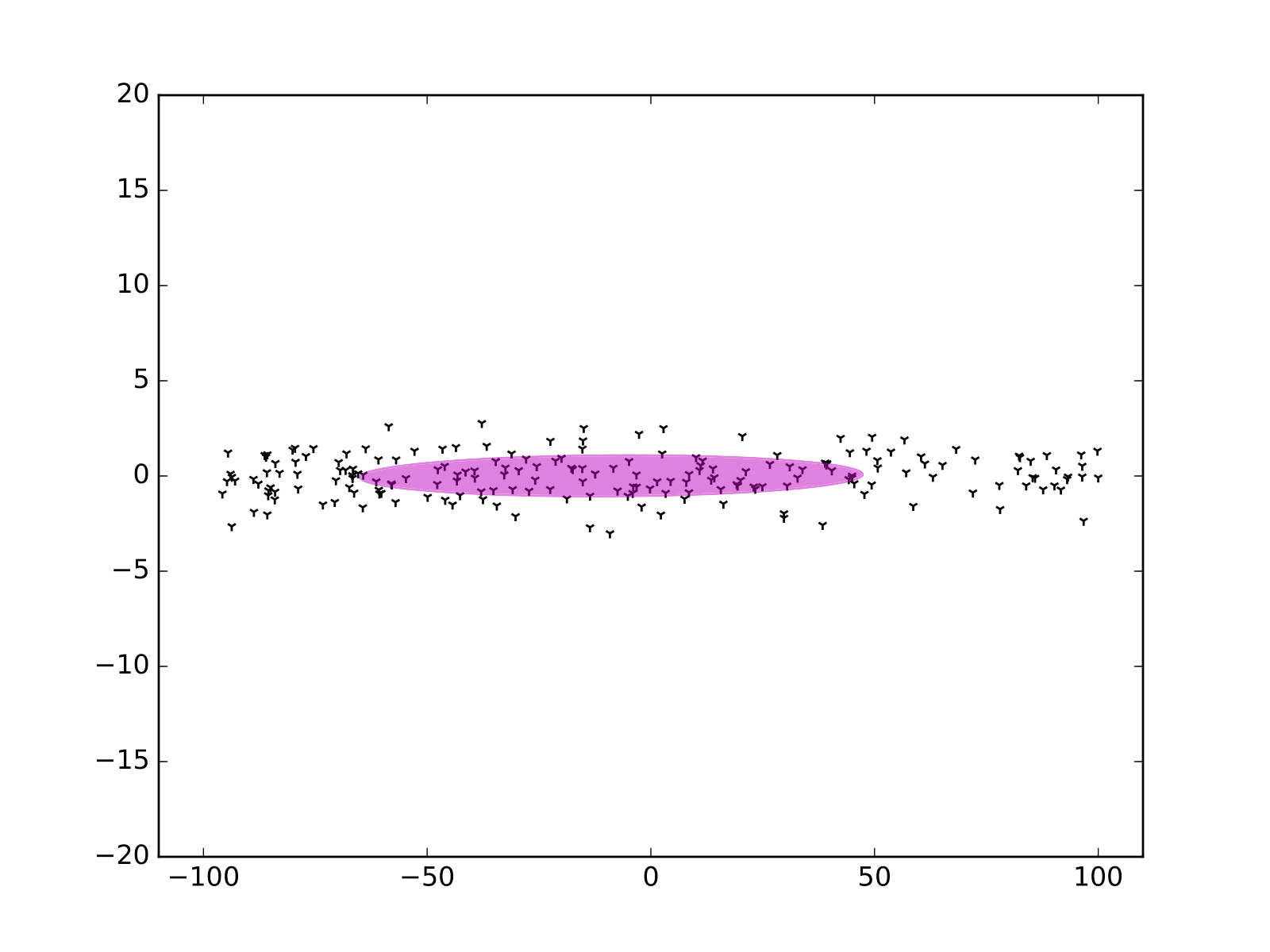
Lidar: PCA - Eigenvectors and eigenvalues
\[ Cov = Q \cdot \Gamma \cdot Q^{-1} \]
\[ Q = \begin{pmatrix} \color{red}{v_1^x} & \color{green}{v_2^x} \\ \color{red}{v_1^y} & \color{green}{v_2^y} \end{pmatrix} \]
\[ \Gamma = \begin{pmatrix} \color{red}{\sigma_1^2} & 0 \\ 0 & \color{green}{\sigma_2^2} \end{pmatrix} \]
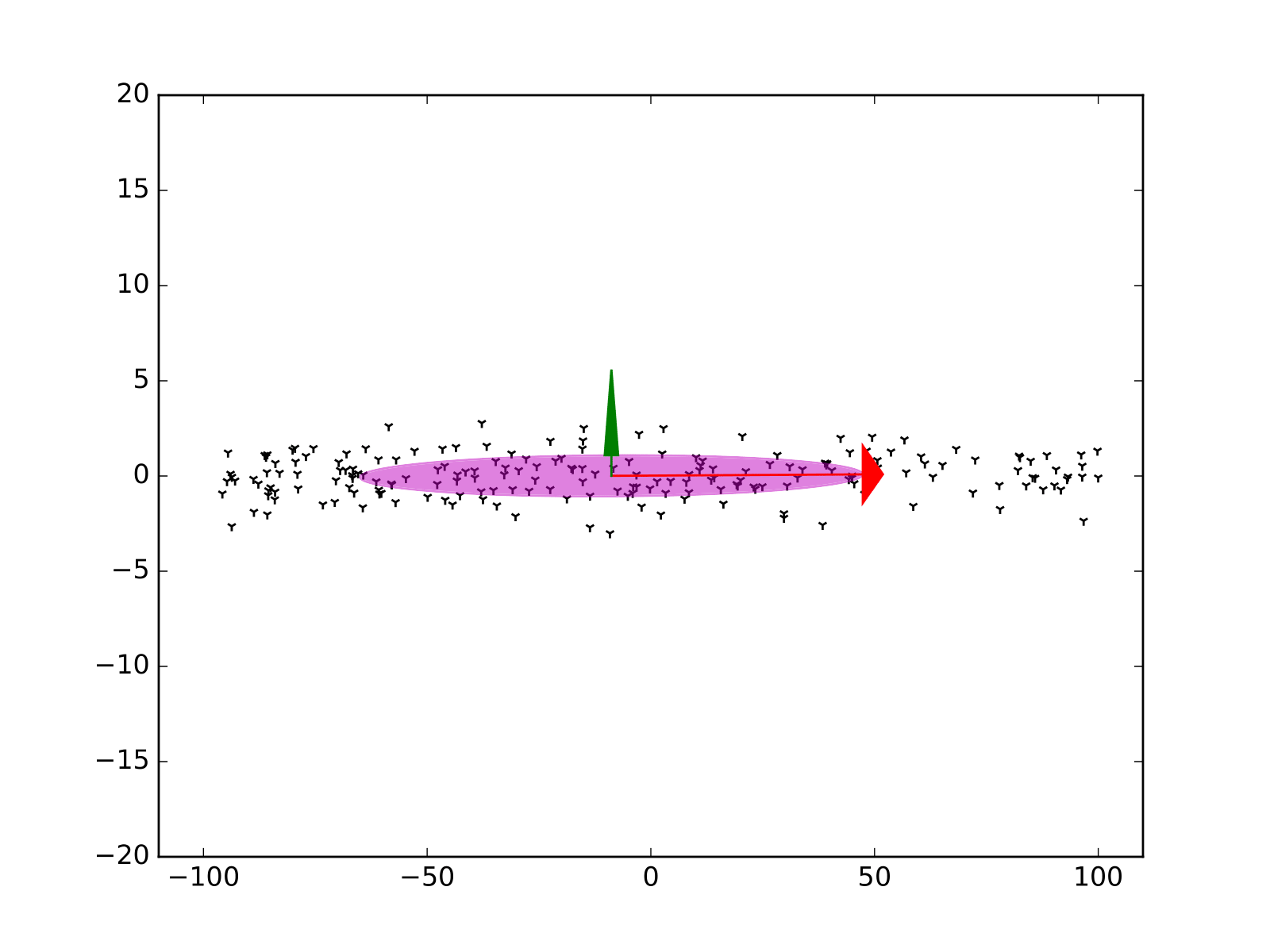
Lidar: PCA - Rules
- Normalized eigenvalues \[\begin{align*} e_1 &= \lambda_1/(\lambda_1+\lambda_2+\lambda_3) \\ e_2 &= \lambda_2/(\lambda_1+\lambda_2+\lambda_3) \\ e_3 &= \lambda_3/(\lambda_1+\lambda_2+\lambda_3) \end{align*}\]
Geometric properties:
- \(linearity = (e_1-e_2)/e_1\)
- \(planarity = (e_2-e_3)/e_1\)
- \(sphericity = e_3/e_1\)
- \(omnivariance = \sqrt[3]{e_1e_2e_3}\)
- \(anisotropy = \frac{e_1-e_3}{e_1}\)
- \(eigenentropy = \sum_{k=1}^3 -e_klog(e_k)\)
- \(surface variation = e_3%\frac{e_3}{\sum_{k=1}^3 e_k}\)
- \(verticality=\left| \frac{\pi}{2} - angle\left(v_z, v_{(1)}\right)\right|%{i\in(0,1,2)}\)
Kalman filter: Lidar measurements
- Detections
\[\begin{align} {}^{\text{L}}\boldsymbol{Y}^{\text{L}}_k = \left\{ \left. {}^{\text{L}}\boldsymbol{y}^{\text{L}}_{k,i} = \left({}^{\text{L}}x^{\text{L}}_{k,i},{}^{\text{L}}y^{\text{L}}_{k,i}\right) \right| i=1,\ldots \right\}, \end{align}\]
- Projections in map frame
\[\begin{align} {}^{\text{O}}\boldsymbol{Y}^{\text{L}}_k = \left\{ \left. {}^{\text{O}}\boldsymbol{y}^{\text{L}}_{k,i} = \left({}^{\text{O}}x^{\text{L}}_{k,i},{}^{\text{O}}y^{\text{L}}_{k,i}\right) \right| i=1,\ldots \right\}, \end{align}\]
- Chosen distance for hungarian method: Mahalanobis distance
\[\begin{equation} \mathcal{D}^{\text{mah}}_{m,y}= \sqrt{(m -y)^\top R^{-1} (m-y)^\top} \end{equation}\]
- Observation model
\[\begin{equation} {}^{\text{L}}\boldsymbol{y}^{\text{L}}_{k,i} = {}^{\text{L}}\boldsymbol{m}_{k,j} + \boldsymbol{\beta}^L_{k,i} \end{equation}\]
- Covariance \(0.25^2\times {I}_{2}\)
Lidar: localization results
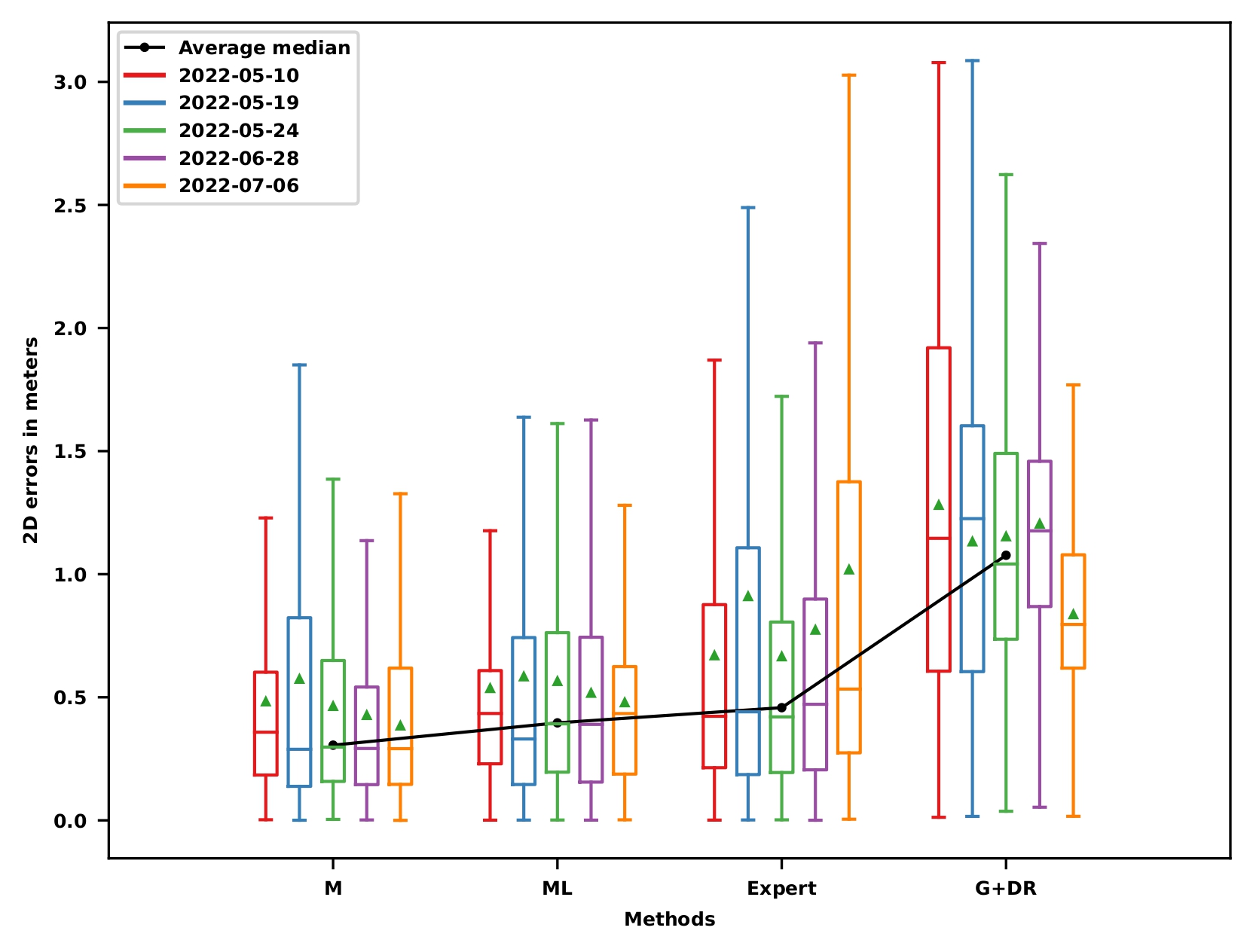
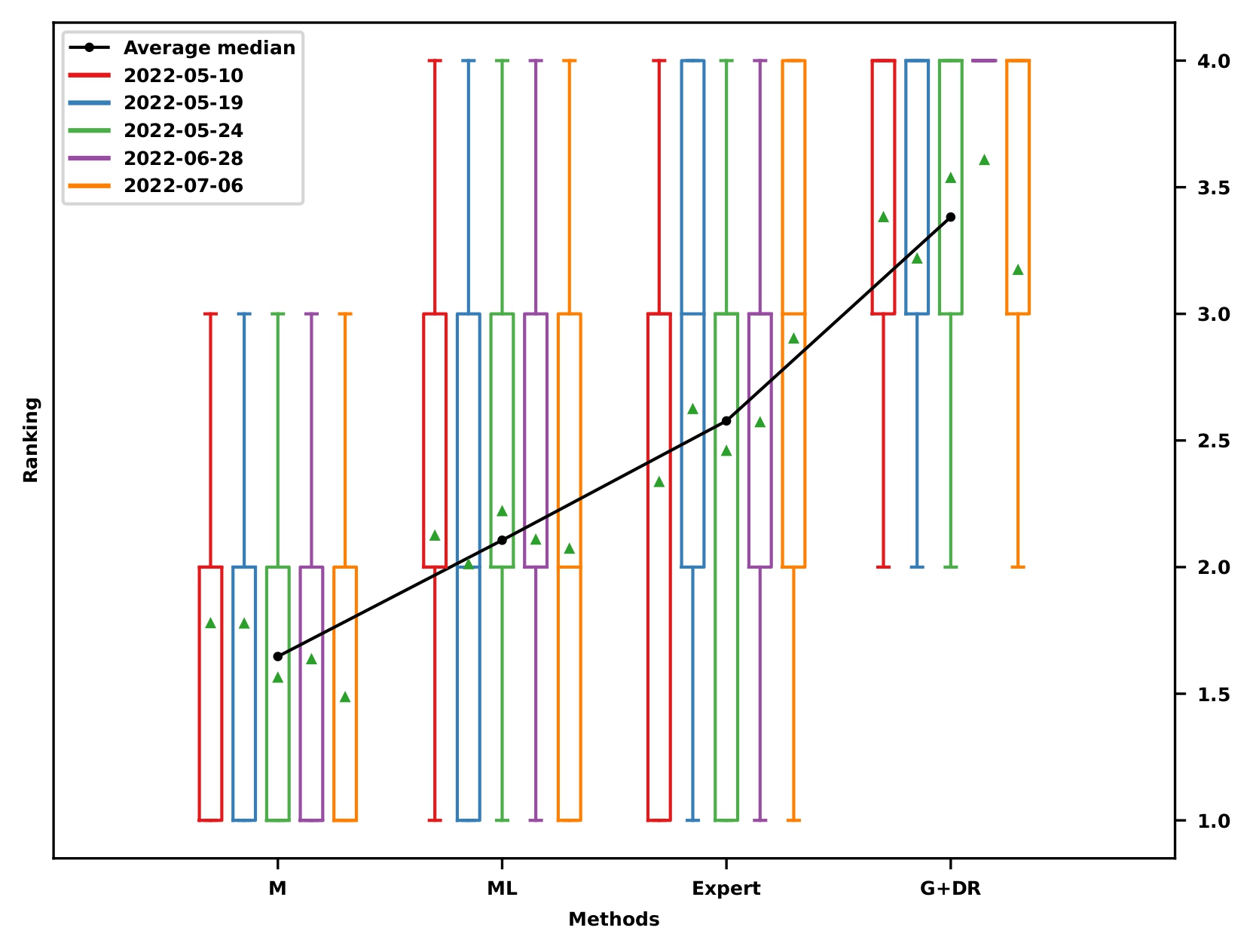
Lidar with motion compensation: localization results
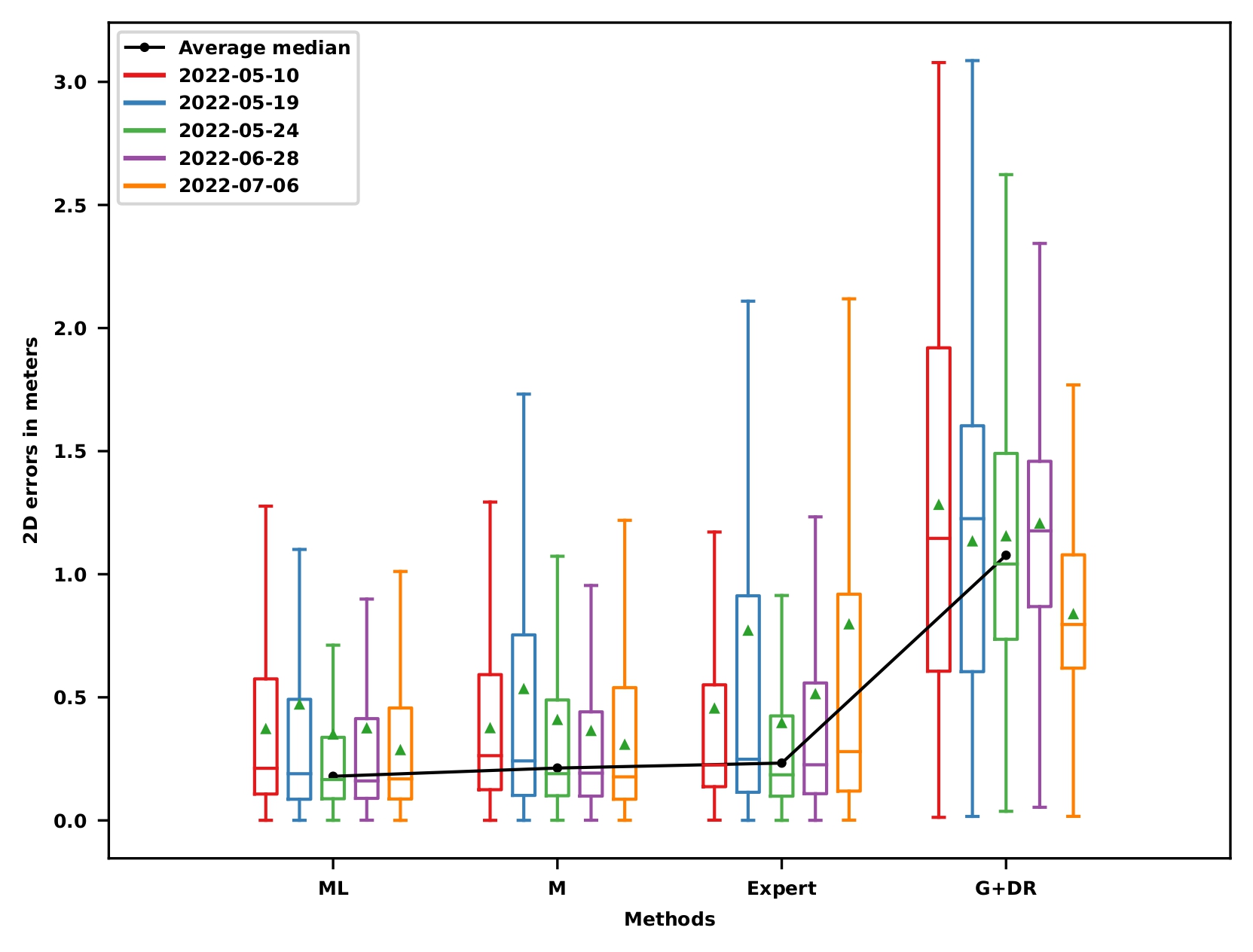
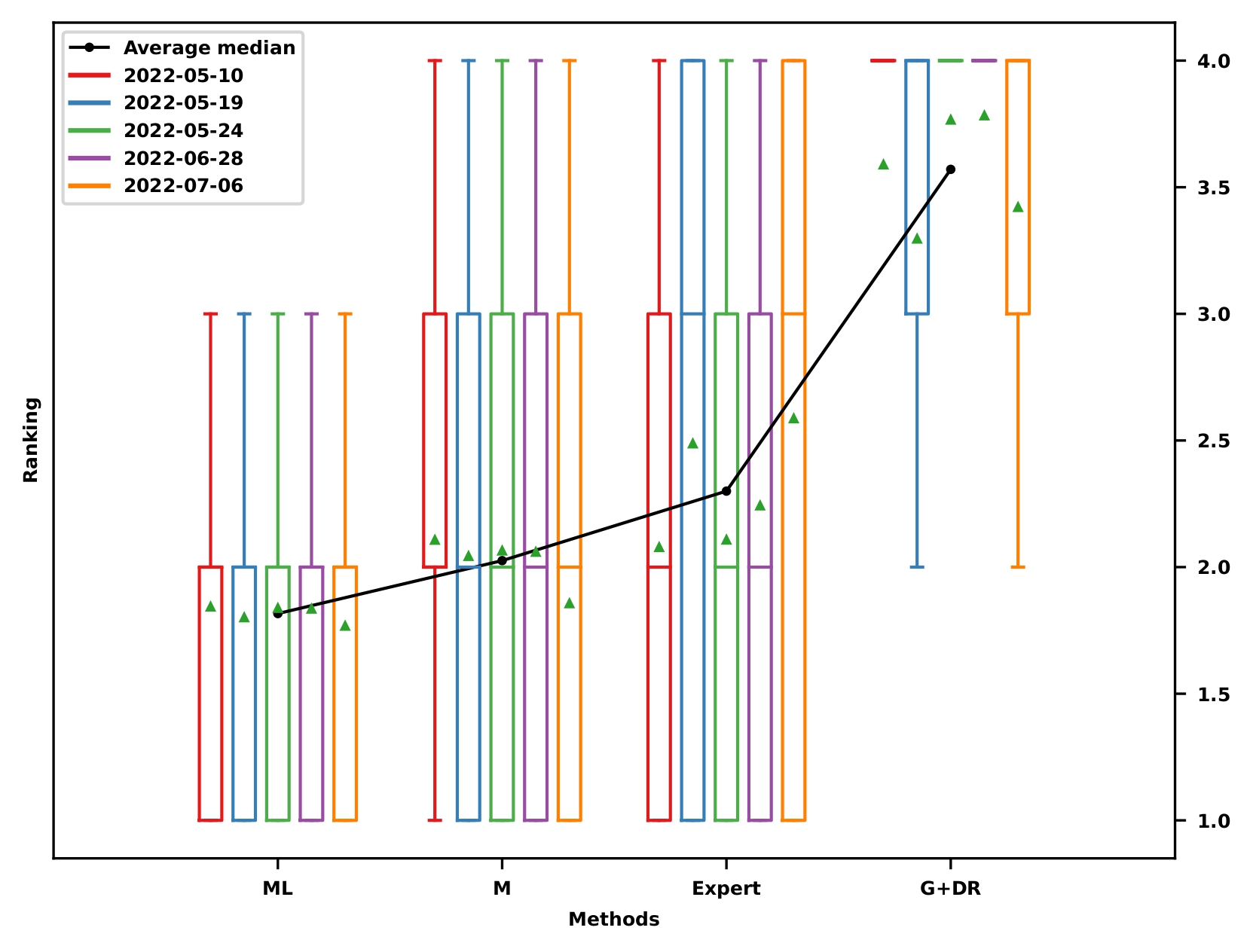
Lidar with motion compensation: Results with PPP-RTK